题目
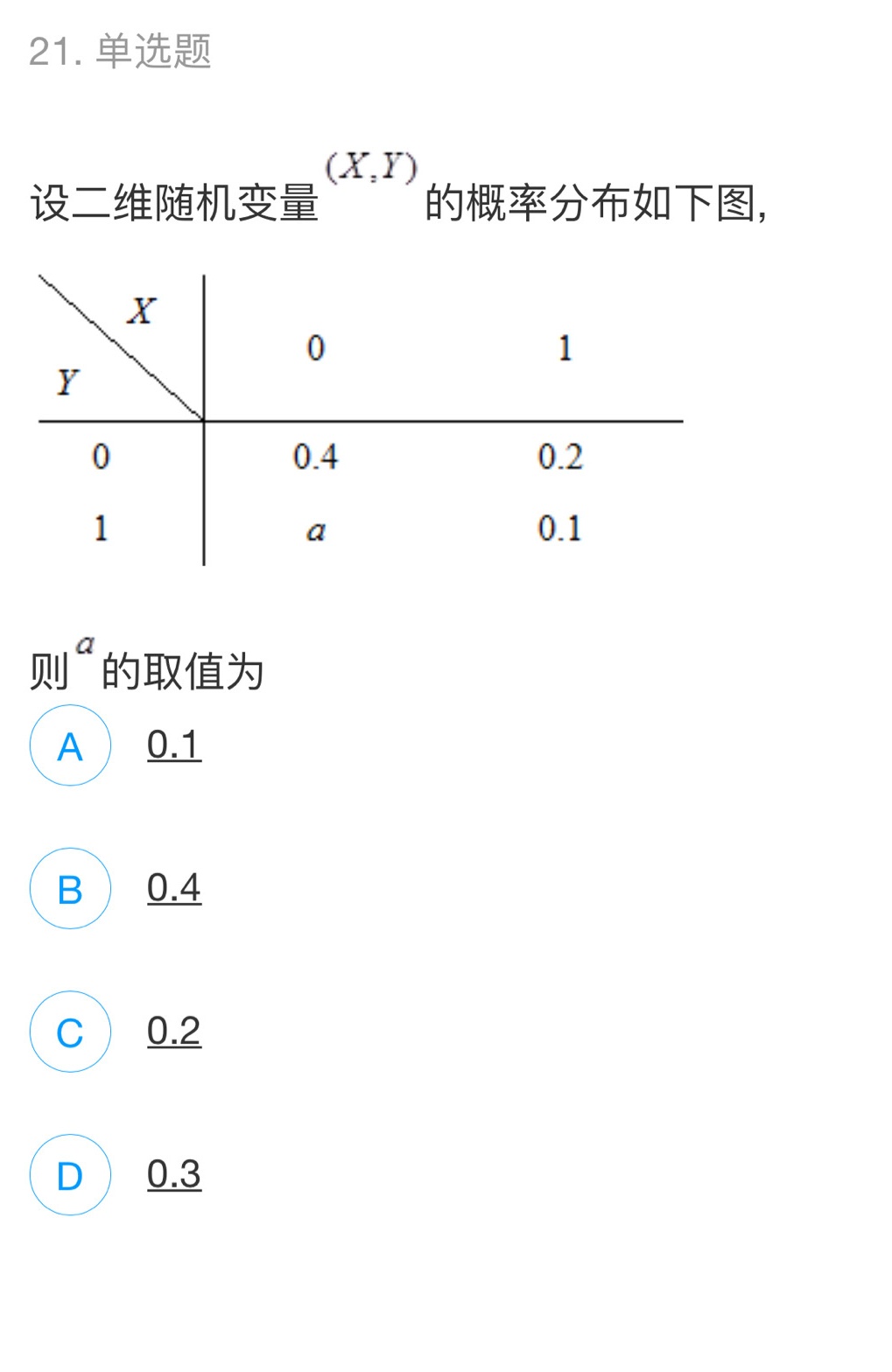
21.单选题-|||-设二维随机变量的概率分布如下图,-|||-x-|||-0 1-|||-Y-|||-0 0.4 0.2-|||-1 a 0.1-|||-则"的取值为-|||-A 0.1-|||-B 0.4-|||-C 0.2-|||-D 0.3
题目解答
答案
∵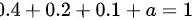
∴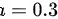
故本题选择(D)
解析
考查要点:本题主要考查二维随机变量概率分布的基本性质,即所有可能取值的概率之和等于1。
解题核心思路:根据概率分布的规范性条件,将表格中所有已知概率相加,再加上未知数$a$,令总和等于1,解方程即可求得$a$的值。
破题关键点:
- 明确二维随机变量概率分布表的结构,确认每个单元格对应的具体概率值。
- 利用概率和为1的性质建立方程,通过代数运算求解未知数。
根据题目给出的概率分布表,二维随机变量$(X,Y)$的取值及对应概率如下:
| X \ Y | 0 | 1 |
|---|---|---|
| 0 | 0.4 | 0.2 |
| 1 | $a$ | 0.1 |
所有概率之和必须等于1,因此可列方程:
$0.4 + 0.2 + a + 0.1 = 1$
解方程步骤:
- 计算已知概率之和:
$0.4 + 0.2 + 0.1 = 0.7$ - 代入方程求$a$:
$0.7 + a = 1 \implies a = 1 - 0.7 = 0.3$
因此,$a$的取值为0.3,对应选项D。