12.(2012全国竞赛)求通过直线L: ) 2x+y-3z+2=0 5x+5y-4z+3=0 . 的两个相互垂直的平面π1-|||-和π2,使其中一个平面过点 (4,-3,1).
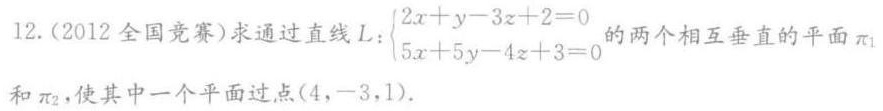
题目解答
答案
解析
本题考查空间解析几何中平面束方程的应用,以及利用平面垂直条件求平面方程的方法,核心思路是通过平面束方程表示过已知直线的所有平面,再结合平面过定点和两平面垂直的条件求解。
步骤1:写出过直线$L$的平面束方程
直线$L$由两个平面$\Pi_1:2x+y-3z+2=0$和$\Pi_2:5x+5y-4z+3=0$交线确定,过$L$的平面束方程为:
$(2x+y-3z+2)+\lambda(5x+5y-4z+3)=0 \quad (\lambda\in\mathbb{R})$
整理得:
$(2+5\lambda)x+(1+5\lambda)y+(-3-4\lambda)z+(2+3\lambda)=0 \quad \text{(1)}$
步骤2:求过点$(4,-3,1)$的平面$\pi_1$
将点$(4,-3,1)$代入方程(1),解得$\lambda$:
$(2+5\lambda)\cdot4+(1+5\lambda)\cdot(-3)+(-3-4\lambda)\cdot1+(2+3\lambda)=0$
展开计算:
$8+20\lambda-3-15\lambda-3-4\lambda+2+3\lambda=0 \implies 4\lambda+4=0 \implies \lambda=-1$
代入$\lambda=-1$得$\pi_1$:
$(2-5)x+(1-5)y+(-3+4)z+(2-3)=0 \implies -3x-4y+z-1=0 \implies 3x+4y-z+1=0$
步骤3:求与$\pi_1$垂直的平面$\pi_2$
$\pi_2$也在平面束中,其法向量为$\vec{n}=(2+5\lambda,1+5\lambda,-3-4\lambda)$。$\pi_1$的法向量为$(3,4,-1)$,垂直条件为$\vec{n}\cdot(3,4,-1)=0$:
$3(2+5\lambda)+4(1+5\lambda)-1(-3-4\lambda)=0$
展开计算:
$6+15\lambda+4+20\lambda+3+4\lambda=0 \implies 39\lambda+13=0 \implies \lambda=-\frac{1}{3}$
代入$\lambda=-\frac{1}{3}$得$\pi_2$:
$\left(2-\frac{5}{3}\right)x+\left(1-\frac{5}{3}\right)y+\left(-3+\frac{4}{3}\right)z+\left(2-1\right)=0$
整理得:
$\frac{1}{3}x-\frac{2}{3}y-\frac{5}{3}z+1=0 \implies x-2y-5z+3=0$