题目
设 f(0)=0 ,f(1)=16 ,f(2)=46 ,则f(x)的二次牛顿插值多项式为-|||-._(2)(x)=16x+7x(x-1)
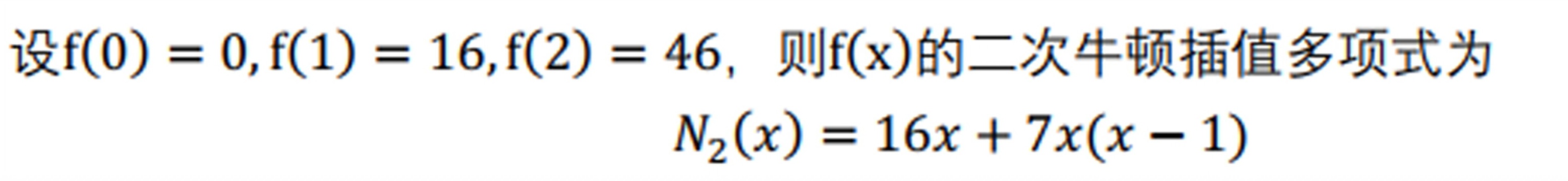
题目解答
答案
正确
解析
本题考查二次牛顿插值多项式的构造与验证,核心是通过给定函数值计算差商表,并利用差商构建插值多项式,最终与题目所给多项式对比判断正确性。
步骤1:明确二次牛顿插值多项式的形式
二次牛顿插值多项式的一般形式为:
$N_2(x) = f[0] + f[0,1](x-0) + f[0,1,2](x-0)(x-1)$
其中:
- $f[0] = f(0)$(零阶差商),
- $f[0,1]$(一阶差商),
- $f[0,1,2]$(二阶差商)。
步骤2:计算各阶差商
已知 $f(0)=0$,$f(1)=16$,$f(2)=46$:
- 零阶差商:$f[0] = f(0) = 0$;
- 一阶差商:
$f[0,1] = \frac{f(1)-f(0)}{1-0} = \frac{16-0}{1} = 16$
$f[1,2] = \frac{f(2)-f(1)}{2-1} = \frac{46-16}{1} = 30$ - 二阶差商:
$f[0,1,2] = \frac{f[1,2]-f[0,1]}{2-0} = \frac{30-16}{2} = 7$
步骤3:构建二次牛顿插值多项式
代入差商:
$N_2(x) = 0 + 16(x-0) + 7(x-0)(x-1) = 16x + 7x(x-1)$
步骤4:对比题目所给多项式
题目给出的多项式为 $N_2(x)=16x+7x(x-1)$,与计算结果完全一致,故正确。