题目
已知f(x)dx=10 (int )_(b)^cf(x)dx=6，则定积分f(x)dx=10 (int )_(b)^cf(x)dx=6的值为( ).A.16B.-4C.-16D.4
已知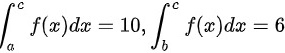
，则定积分
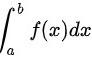的值为( ).
A.16
B.-4
C.-16
D.4
题目解答
答案
我们需要知道：
定积分的性质：
定积分的积分区间具有可加性：
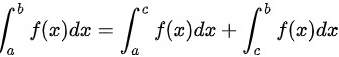
已知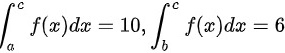，则定积分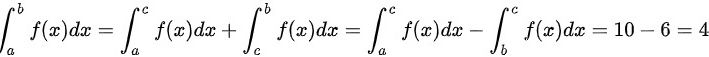
;故正确答案为：D
解析
步骤 1：理解定积分的性质
定积分的积分区间具有可加性，即${\int }_{a}^{b}f(x)dx={\int }_{a}^{c}f(x)dx+{\int }_{c}^{b}f(x)dx$。这里需要注意的是，当积分区间从c到b时，积分值的符号会与从b到c时相反，即${\int }_{c}^{b}f(x)dx=-{\int }_{b}^{c}f(x)dx$。
步骤 2：应用定积分的性质
根据题目给出的条件，${\int }_{a}^{c}f(x)dx=10$，${\int }_{b}^{c}f(x)dx=6$。我们需要求${\int }_{a}^{b}f(x)dx$的值。根据定积分的性质，${\int }_{a}^{b}f(x)dx={\int }_{a}^{c}f(x)dx+{\int }_{c}^{b}f(x)dx$。将已知条件代入，得到${\int }_{a}^{b}f(x)dx=10+(-6)=4$。
步骤 3：得出结论
根据上述计算，${\int }_{a}^{b}f(x)dx$的值为4。
定积分的积分区间具有可加性，即${\int }_{a}^{b}f(x)dx={\int }_{a}^{c}f(x)dx+{\int }_{c}^{b}f(x)dx$。这里需要注意的是，当积分区间从c到b时，积分值的符号会与从b到c时相反，即${\int }_{c}^{b}f(x)dx=-{\int }_{b}^{c}f(x)dx$。
步骤 2：应用定积分的性质
根据题目给出的条件，${\int }_{a}^{c}f(x)dx=10$，${\int }_{b}^{c}f(x)dx=6$。我们需要求${\int }_{a}^{b}f(x)dx$的值。根据定积分的性质，${\int }_{a}^{b}f(x)dx={\int }_{a}^{c}f(x)dx+{\int }_{c}^{b}f(x)dx$。将已知条件代入，得到${\int }_{a}^{b}f(x)dx=10+(-6)=4$。
步骤 3：得出结论
根据上述计算，${\int }_{a}^{b}f(x)dx$的值为4。