题目
利用极限存在准则证明:(1) lim _(narrow infty )sqrt (1+dfrac {1)(n)}=1
利用极限存在准则证明:
(1) 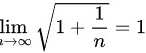
题目解答
答案
证明 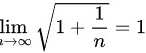
可先对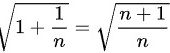 进行放缩
进行放缩
而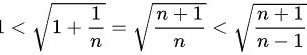
(1)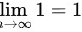
(2)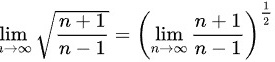
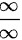 型极限可以使用洛必达,而根据数列与函数的子列与母列的关系
型极限可以使用洛必达,而根据数列与函数的子列与母列的关系
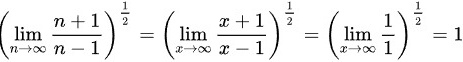
根据夹逼准则可知, 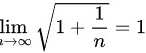
解析
考查要点:本题主要考查利用夹逼准则(极限存在准则之一)证明数列极限的方法,以及对数列放缩技巧的掌握。
解题核心思路:
- 构造不等式链:将原式$\sqrt{1+\dfrac{1}{n}}$夹在两个易于求极限的数列之间。
- 证明上下界极限相同:通过变形和化简,分别求出上下界的极限值,并验证它们的极限均为$1$。
- 应用夹逼准则:根据夹逼准则,原数列的极限也为$1$。
破题关键点:
- 分母放缩:将分母$n$适当放大为$n-1$,构造更大的分数$\dfrac{n+1}{n-1}$,从而得到上界。
- 极限化简:对上界$\sqrt{\dfrac{n+1}{n-1}}$进行变形,利用$\dfrac{n+1}{n-1} = 1 + \dfrac{2}{n-1}$化简极限。
第(1)题
步骤1:变形原式
将原式改写为:
$\sqrt{1+\dfrac{1}{n}} = \sqrt{\dfrac{n+1}{n}}.$
步骤2:构造不等式链
通过分母放缩,构造上下界:
$1 < \sqrt{\dfrac{n+1}{n}} < \sqrt{\dfrac{n+1}{n-1}}.$
步骤3:求下界极限
显然,当$n \rightarrow \infty$时,下界$1$的极限为$1$。
步骤4:求上界极限
对上界$\sqrt{\dfrac{n+1}{n-1}}$进行变形:
$\dfrac{n+1}{n-1} = 1 + \dfrac{2}{n-1}.$
当$n \rightarrow \infty$时,$\dfrac{2}{n-1} \rightarrow 0$,因此:
$\lim_{n \rightarrow \infty} \sqrt{\dfrac{n+1}{n-1}} = \sqrt{1 + 0} = 1.$
步骤5:应用夹逼准则
由于上下界的极限均为$1$,根据夹逼准则,原数列的极限也为$1$。