题目
设向量0 1 2-|||-(alpha )_(1)= 1 _(2)= 1 ,beta = 1-|||--1 1 3，则0 1 2-|||-(alpha )_(1)= 1 _(2)= 1 ,beta = 1-|||--1 1 3中系数0 1 2-|||-(alpha )_(1)= 1 _(2)= 1 ,beta = 1-|||--1 1 3的取值为（）A 0 1 2-|||-(alpha )_(1)= 1 _(2)= 1 ,beta = 1-|||--1 1 3B 0 1 2-|||-(alpha )_(1)= 1 _(2)= 1 ,beta = 1-|||--1 1 3C 0 1 2-|||-(alpha )_(1)= 1 _(2)= 1 ,beta = 1-|||--1 1 3D0 1 2-|||-(alpha )_(1)= 1 _(2)= 1 ,beta = 1-|||--1 1 3
设向量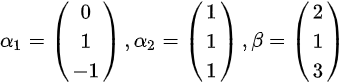
，则
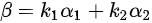中系数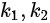
的取值为（）
A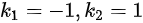 
B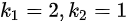 
C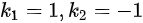 
D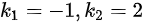
题目解答
答案
本题答案选D
已知向量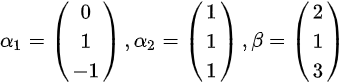
且满足等式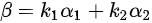成立
则有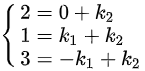
解得：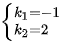
解析
步骤 1：建立方程组
根据题目条件，向量$\beta$可以表示为向量${\alpha }_{1}$和${\alpha }_{2}$的线性组合，即$\beta ={k}_{1}{\alpha }_{1}+{k}_{2}{\alpha }_{2}$。将已知向量代入，得到方程组：
$\left \{ \begin{matrix} 2=0+{k}_{2}\\ 1={k}_{1}+{k}_{2}\\ 3=-{k}_{1}+{k}_{2}\end{matrix} \right.$
步骤 2：求解方程组
从第一个方程中，可以直接得到${k}_{2}=2$。将${k}_{2}=2$代入第二个方程，得到${k}_{1}+2=1$，从而${k}_{1}=-1$。最后，验证第三个方程是否成立，将${k}_{1}=-1$和${k}_{2}=2$代入，得到$3=-(-1)+2$，即$3=3$，方程成立。
步骤 3：验证答案
根据求解结果，${k}_{1}=-1$，${k}_{2}=2$，符合题目要求。
根据题目条件，向量$\beta$可以表示为向量${\alpha }_{1}$和${\alpha }_{2}$的线性组合，即$\beta ={k}_{1}{\alpha }_{1}+{k}_{2}{\alpha }_{2}$。将已知向量代入，得到方程组：
$\left \{ \begin{matrix} 2=0+{k}_{2}\\ 1={k}_{1}+{k}_{2}\\ 3=-{k}_{1}+{k}_{2}\end{matrix} \right.$
步骤 2：求解方程组
从第一个方程中，可以直接得到${k}_{2}=2$。将${k}_{2}=2$代入第二个方程，得到${k}_{1}+2=1$，从而${k}_{1}=-1$。最后，验证第三个方程是否成立，将${k}_{1}=-1$和${k}_{2}=2$代入，得到$3=-(-1)+2$，即$3=3$，方程成立。
步骤 3：验证答案
根据求解结果，${k}_{1}=-1$，${k}_{2}=2$，符合题目要求。