题目
下列各组函数中，是相同的函数的是（）。A (x)=ln (x)^2 和 (x)=2ln x-|||-B f(x)=|x| 和 (x)=sqrt ({x)^2}-|||-C f(x)=x 和 (x)=((sqrt {x))}^2-|||-D (x)=dfrac (|x|)(x) 和 g(x)=1A、AB、BC、CD、D
下列各组函数中，是相同的函数的是（）。
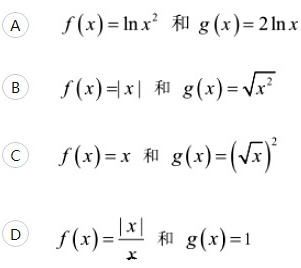
- A、A
- B、B
- C、C
- D、D
题目解答
答案
B. $f(x)=|x| 和 $g(x)=\sqrt {{x}^{2}}$
解析
步骤 1：分析函数 $f(x)=\ln {x}^{2}$ 和 $g(x)=2\ln x$
函数 $f(x)=\ln {x}^{2}$ 的定义域为 $x \neq 0$，而 $g(x)=2\ln x$ 的定义域为 $x > 0$。因此，这两个函数的定义域不同，所以它们不是相同的函数。
步骤 2：分析函数 $f(x)=|x|$ 和 $g(x)=\sqrt {{x}^{2}}$
函数 $f(x)=|x|$ 和 $g(x)=\sqrt {{x}^{2}}$ 的定义域都是全体实数，且对于任意的 $x$，都有 $|x| = \sqrt {{x}^{2}}$。因此，这两个函数是相同的函数。
步骤 3：分析函数 $f(x)=x$ 和 $g(x)={(\sqrt {x})}^{2}$
函数 $f(x)=x$ 的定义域为全体实数，而 $g(x)={(\sqrt {x})}^{2}$ 的定义域为 $x \geq 0$。因此，这两个函数的定义域不同，所以它们不是相同的函数。
步骤 4：分析函数 $f(x)=\dfrac {|x|}{x}$ 和 $g(x)=1$
函数 $f(x)=\dfrac {|x|}{x}$ 的定义域为 $x \neq 0$，且对于 $x > 0$，$f(x)=1$；对于 $x < 0$，$f(x)=-1$。而 $g(x)=1$ 的定义域为全体实数。因此，这两个函数的定义域和对应关系都不同，所以它们不是相同的函数。
函数 $f(x)=\ln {x}^{2}$ 的定义域为 $x \neq 0$，而 $g(x)=2\ln x$ 的定义域为 $x > 0$。因此，这两个函数的定义域不同，所以它们不是相同的函数。
步骤 2：分析函数 $f(x)=|x|$ 和 $g(x)=\sqrt {{x}^{2}}$
函数 $f(x)=|x|$ 和 $g(x)=\sqrt {{x}^{2}}$ 的定义域都是全体实数，且对于任意的 $x$，都有 $|x| = \sqrt {{x}^{2}}$。因此，这两个函数是相同的函数。
步骤 3：分析函数 $f(x)=x$ 和 $g(x)={(\sqrt {x})}^{2}$
函数 $f(x)=x$ 的定义域为全体实数，而 $g(x)={(\sqrt {x})}^{2}$ 的定义域为 $x \geq 0$。因此，这两个函数的定义域不同，所以它们不是相同的函数。
步骤 4：分析函数 $f(x)=\dfrac {|x|}{x}$ 和 $g(x)=1$
函数 $f(x)=\dfrac {|x|}{x}$ 的定义域为 $x \neq 0$，且对于 $x > 0$，$f(x)=1$；对于 $x < 0$，$f(x)=-1$。而 $g(x)=1$ 的定义域为全体实数。因此，这两个函数的定义域和对应关系都不同，所以它们不是相同的函数。