题目
函数(x)=sin (2x+dfrac (pi )(6))的最小正周期为 .
函数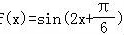 的最小正周期为 .
的最小正周期为 .
题目解答
答案
π
解析
考查要点:本题主要考查正弦函数的周期性,特别是当函数形式为$\sin(Bx + C)$时,如何确定其最小正周期。
解题核心思路:对于函数$f(x) = \sin(Bx + C)$,其最小正周期由系数$B$决定,与相位项$C$无关。关键公式为周期$T = \dfrac{2\pi}{|B|}$。
破题关键点:
- 识别题目中的$B$值(本题中$B=2$)。
- 直接代入公式计算周期,无需考虑相位项$\dfrac{\pi}{6}$的影响。
对于函数$f(x) = \sin(2x + \dfrac{\pi}{6})$,其形式为$\sin(Bx + C)$,其中:
- 系数$B = 2$
- 相位项$C = \dfrac{\pi}{6}$
根据正弦函数的周期公式:
$T = \dfrac{2\pi}{|B|}$
代入$B = 2$得:
$T = \dfrac{2\pi}{2} = \pi$
结论:函数的最小正周期为$\pi$。