题目
设 _(1)=x(e)^x, y2=(x+1)e x, y3=e^(2x)+ x∈^x为某二阶线性非齐次微分方程的三个特解 则该方程的通解为().其中 _(1)=x(e)^x, y2=(x+1)e x, y3=e^(2x)+ x∈^x为任意常数(A) _(1)=x(e)^x, y2=(x+1)e x, y3=e^(2x)+ x∈^x(B) _(1)=x(e)^x, y2=(x+1)e x, y3=e^(2x)+ x∈^x(C) _(1)=x(e)^x, y2=(x+1)e x, y3=e^(2x)+ x∈^x(D) _(1)=x(e)^x, y2=(x+1)e x, y3=e^(2x)+ x∈^x
设 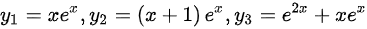 为某二阶线性非齐次微分方程的三个特解 则该方程的通解为().其中
为某二阶线性非齐次微分方程的三个特解 则该方程的通解为().其中 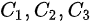 为任意常数
为任意常数
(A) 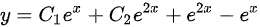
(B) 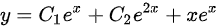
(C) 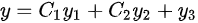
(D) 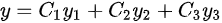
题目解答
答案
解:
将三个特解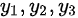 ,代入原微分方程,得到:
,代入原微分方程,得到: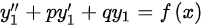 ,
,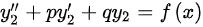 ,
,
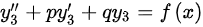 ,
,
其中任意两式相减
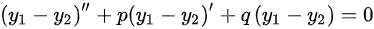
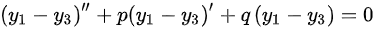 ,
,
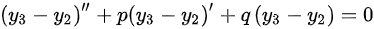
因此得到二阶齐次微分方程的通解为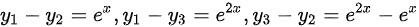 ,
,
进而得到通解结构为: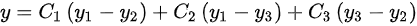
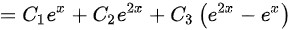
所以选项中A符合上述形式,因此正确答案选:A
解析
本题考查二阶线性非齐次微分方程的通解结构。解题核心在于:
- 非齐次方程的通解由对应齐次方程的通解加上一个特解构成;
- 齐次方程的解空间可通过非齐次方程的特解之差确定;
- 线性无关解的组合需符合二阶方程的解的结构特点。
关键步骤:
- 通过特解之差构造齐次方程的解;
- 确定齐次方程的基本解系;
- 组合齐次解与特解得到通解。
步骤1:构造齐次方程的解
设非齐次方程为 $y'' + p(x)y' + q(x)y = f(x)$,已知三个特解 $y_1, y_2, y_3$,则:
- $y_1 - y_2 = -e^x$ 是齐次方程的解;
- $y_1 - y_3 = -e^{2x}$ 是齐次方程的解;
- $y_3 - y_2 = e^{2x} - e^x$ 是齐次方程的解。
步骤2:确定齐次方程的基本解系
齐次方程的两个线性无关解为 $e^x$ 和 $e^{2x}$,因此齐次通解为:
$y_h = C_1 e^x + C_2 e^{2x}$
步骤3:构造非齐次方程的通解
任取一个非齐次方程的特解(如 $y_3$),但需注意 $y_3$ 可分解为齐次解与特解的组合。通过分析选项,特解部分为 $e^{2x} - e^x$,因此通解为:
$y = C_1 e^x + C_2 e^{2x} + (e^{2x} - e^x)$
步骤4:匹配选项
选项A的结构符合上述形式,其他选项因常数数量或特解形式错误被排除。