题目
9.求下列函数的全微分:-|||-(1) =ysin (x+y);

题目解答
答案
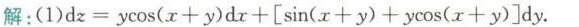
解析
考查要点:本题主要考查二元函数全微分的计算方法,需要掌握偏导数的求导规则以及全微分的表达式形式。
解题核心思路:
- 分别对变量$x$和$y$求偏导数,其中对$x$求偏导时将$y$视为常数,对$y$求偏导时将$x$视为常数。
- 应用乘积法则和链式法则处理复合函数的导数。
- 组合偏导数与微分$dx$、$dy$,得到全微分表达式。
破题关键点:
- 对$y \sin(x+y)$中的$y$和$\sin(x+y)$正确应用乘积法则。
- 在对$y$求偏导时,注意$\sin(x+y)$对$y$的导数需要链式法则。
第(1)题
函数:$z = y \sin(x + y)$
步骤1:求$\frac{\partial z}{\partial x}$
将$y$视为常数,对$x$求导:
$\frac{\partial z}{\partial x} = y \cdot \cos(x + y) \cdot \frac{\partial}{\partial x}(x + y) = y \cos(x + y)$
步骤2:求$\frac{\partial z}{\partial y}$
将$x$视为常数,对$y$求导,需应用乘积法则:
$\frac{\partial z}{\partial y} = \sin(x + y) \cdot \frac{\partial}{\partial y}(y) + y \cdot \cos(x + y) \cdot \frac{\partial}{\partial y}(x + y)$
化简得:
$\frac{\partial z}{\partial y} = \sin(x + y) + y \cos(x + y)$
步骤3:组合全微分
根据全微分公式:
$dz = \frac{\partial z}{\partial x} dx + \frac{\partial z}{\partial y} dy$
代入偏导数结果:
$dz = y \cos(x + y) dx + \left[ \sin(x + y) + y \cos(x + y) \right] dy$