已知一元二次函数的图像的顶点坐标为,并且经过点,求:(1)函数的解析式;(2)函数图像的对称轴;(3)函数单调递减的区间。
已知一元二次函数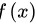 的图像的顶点坐标为
的图像的顶点坐标为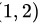 ,并且经过点
,并且经过点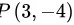 ,求:
,求:
(1)函数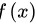 的解析式;
的解析式;
(2)函数图像的对称轴;
(3)函数单调递减的区间。
题目解答
答案
(1)
一元二次函数有三种表达式:
通用式: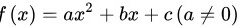
顶点式: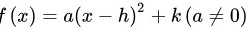
双根式: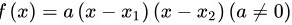
题设给出了顶点坐标,
因此可以设一元二次函数为顶点式:
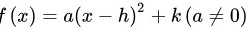
其中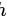 是一元二次函数的顶点横坐标,
是一元二次函数的顶点横坐标,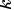 是一元二次函数的顶点纵坐标。
是一元二次函数的顶点纵坐标。
因为顶点坐标为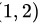 ,
,
所以一元二次函数为:
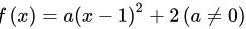
又因为点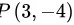 在
在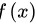 上,
上,
所以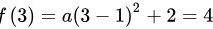
解得
所以函数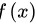 的解析式为:
的解析式为:
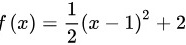
(2)
一元二次函数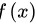 的对称轴为顶点
的对称轴为顶点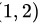 所在的横坐标并与x轴垂直的直线,
所在的横坐标并与x轴垂直的直线,
所以函数图像的对称轴为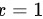
(3)
由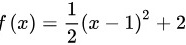 求导得
求导得
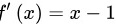
令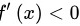 ,即
,即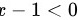 ,
,
得到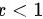
所以函数单调递减的区间为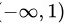
解析
考查要点:本题主要考查一元二次函数的顶点式求法、对称轴的确定以及函数单调性的判断。
解题思路:
- 顶点式应用:已知顶点坐标时,优先使用顶点式$f(x)=a(x-h)^2 +k$,代入顶点坐标后,再利用已知点求参数$a$。
- 对称轴性质:一元二次函数的对称轴为直线$x=h$,直接由顶点横坐标确定。
- 单调性分析:通过导数或抛物线开口方向判断单调区间。开口方向由$a$的符号决定:$a>0$时开口向上,对称轴左侧递减;$a<0$时开口向下,对称轴左侧递增。
关键点:
- 顶点式代入点求参数:代入已知点坐标解方程。
- 导数与单调性关系:导数符号决定函数增减趋势。
第(1)题
步骤1:设顶点式
已知顶点$(1,2)$,设函数为:
$f(x) = a(x-1)^2 + 2$
步骤2:代入点$P(3,-4)$求$a$
将$x=3$,$f(x)=-4$代入方程:
$-4 = a(3-1)^2 + 2 \implies -4 = 4a + 2 \implies 4a = -6 \implies a = -\dfrac{3}{2}$
步骤3:写出解析式
将$a=-\dfrac{3}{2}$代入顶点式:
$f(x) = -\dfrac{3}{2}(x-1)^2 + 2$
第(2)题
对称轴公式
一元二次函数的对称轴为顶点横坐标对应的直线:
$x = 1$
第(3)题
步骤1:求导数
对$f(x)$求导:
$f'(x) = 2 \cdot \left(-\dfrac{3}{2}\right)(x-1) = -3(x-1)$
步骤2:确定单调递减区间
令$f'(x) < 0$:
$-3(x-1) < 0 \implies x-1 > 0 \implies x > 1$
因此,函数在区间$(1, +\infty)$上单调递减。