题目
设事件A和B互不相容,且P(A)= 0.3,P(B)= 0.5,求以下事件的概率:(1)A与B中至少有一个发生;(2)A和B都发生;(3)A发生但B不发生.
设事件A和B互不相容,且P(A)= 0.3,P(B)= 0.5,求以下事件的概率:
(1)A与B中至少有一个发生;
(2)A和B都发生;
(3)A发生但B不发生.
题目解答
答案
∵事件A和B互不相容,且P(A)= 0.3,P(B)= 0.5
(1)事件“A与B中至少有一个发生”可表示为AUB
∴P(AUB)=P(A)+P(B)-P(AB)=P(A)+P(B)=0.3+0.5=0.8
(2)∵事件A和B互不相容
∴A和B不可能同时发生
∴P(AB)=P(∅)=0
(3)事件“A发生但B不发生”可表示为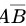
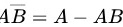
∴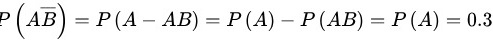
解析
考查要点:本题主要考查互不相容事件的概率计算,涉及并事件、交事件、差事件的概率公式应用。
解题核心思路:
- 互不相容事件的定义是关键:两事件不能同时发生,即$P(AB)=0$。
- 并事件概率:利用互不相容时的加法公式$P(A \cup B) = P(A) + P(B)$。
- 差事件概率:$P(A \text{发生但} B \text{不发生}) = P(A) - P(AB)$,因$P(AB)=0$,结果直接为$P(A)$。
第(1)题
事件“A与B中至少有一个发生”对应并事件$A \cup B$。
应用互不相容性质
因$A$与$B$互不相容,$P(AB)=0$,故并事件概率为:
$P(A \cup B) = P(A) + P(B) - P(AB) = 0.3 + 0.5 - 0 = 0.8$
第(2)题
事件“A和B都发生”对应交事件$AB$。
直接应用互不相容性质
互不相容事件的交集为空集,故:
$P(AB) = P(\varnothing) = 0$
第(3)题
事件“A发生但B不发生”可表示为$A \cap \overline{B}$(或$A - AB$)。
计算差事件概率
根据公式:
$P(A \cap \overline{B}) = P(A) - P(AB)$
因$P(AB)=0$,代入得:
$P(A \cap \overline{B}) = 0.3 - 0 = 0.3$