题目
设随机变量X的分布列为:x -2 0 2-|||-P 0.4 0.3 0.3求E(X),E(X^2),E(3X^2+5)。
设随机变量$$X$$的分布列为:
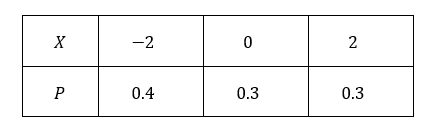
求$$E(X)$$,$$E(X^2)$$,$$E(3X^2+5)$$。
题目解答
答案
$$-0.2$$;$$2.8$$;$$13.4$$
解析
步骤 1:计算$$E(X)$$
根据随机变量的期望公式,$$E(X) = \sum_{i} x_i \cdot P(x_i)$$,其中$$x_i$$是随机变量的取值,$$P(x_i)$$是对应的概率。将题目中给出的分布列代入公式计算。
步骤 2:计算$$E(X^2)$$
根据随机变量函数的期望公式,$$E(g(X)) = \sum_{i} g(x_i) \cdot P(x_i)$$,其中$$g(X)$$是随机变量的函数。将$$g(X) = X^2$$代入公式计算。
步骤 3:计算$$E(3X^2+5)$$
根据随机变量函数的期望公式,$$E(g(X)) = \sum_{i} g(x_i) \cdot P(x_i)$$,其中$$g(X) = 3X^2+5$$。将$$g(X) = 3X^2+5$$代入公式计算。
根据随机变量的期望公式,$$E(X) = \sum_{i} x_i \cdot P(x_i)$$,其中$$x_i$$是随机变量的取值,$$P(x_i)$$是对应的概率。将题目中给出的分布列代入公式计算。
步骤 2:计算$$E(X^2)$$
根据随机变量函数的期望公式,$$E(g(X)) = \sum_{i} g(x_i) \cdot P(x_i)$$,其中$$g(X)$$是随机变量的函数。将$$g(X) = X^2$$代入公式计算。
步骤 3:计算$$E(3X^2+5)$$
根据随机变量函数的期望公式,$$E(g(X)) = \sum_{i} g(x_i) \cdot P(x_i)$$,其中$$g(X) = 3X^2+5$$。将$$g(X) = 3X^2+5$$代入公式计算。