题目
(17)(本题满分10分)-|||-设函数 y=y(x) 是微分方程 '+dfrac (1)(2sqrt {x)}y=2+sqrt (x) 的满足 y(1)=3 的解,求曲线 y=-|||-y(x)的渐近线.
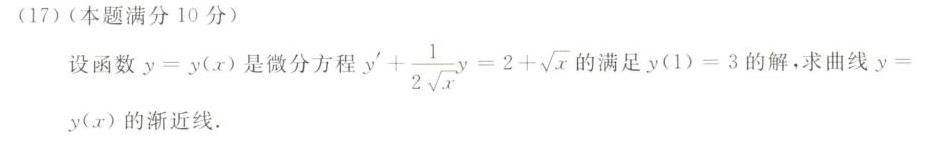
题目解答
答案
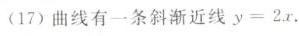
解析
考查要点:本题主要考查一阶线性微分方程的解法及函数渐近线的求解方法。
解题核心思路:
- 识别微分方程类型:题目给出的方程为一阶线性微分方程,标准形式为$y' + P(x)y = Q(x)$,需使用积分因子法求解。
- 求解微分方程:通过计算积分因子,将方程转化为可直接积分的形式,得到通解后利用初始条件确定特解。
- 分析渐近线:对特解函数进行极限分析,判断当$x \to +\infty$时函数的行为,确定斜渐近线。
破题关键点:
- 积分因子的计算:正确计算积分因子$\mu(x) = e^{\int \frac{1}{2\sqrt{x}} dx}$。
- 积分过程:对右侧积分$\int e^{\sqrt{x}} (2 + \sqrt{x}) dx$需分部积分多次,注意代数化简。
- 渐近线判定:当$x \to +\infty$时,特解中的指数项$e^{1 - \sqrt{x}}$趋近于$0$,剩余项$2x$决定斜渐近线。
求解微分方程
-
确定积分因子
方程的标准形式为:
$y' + \frac{1}{2\sqrt{x}} y = 2 + \sqrt{x}$
积分因子为:
$\mu(x) = e^{\int \frac{1}{2\sqrt{x}} dx} = e^{\sqrt{x}}$ -
方程变形与积分
两边乘以积分因子:
$e^{\sqrt{x}} y' + \frac{e^{\sqrt{x}}}{2\sqrt{x}} y = e^{\sqrt{x}} (2 + \sqrt{x})$
左侧为$\frac{d}{dx} \left( e^{\sqrt{x}} y \right)$,积分得:
$e^{\sqrt{x}} y = \int e^{\sqrt{x}} (2 + \sqrt{x}) dx + C$ -
计算右侧积分
通过变量代换$t = \sqrt{x}$,分部积分后化简得:
$\int e^{\sqrt{x}} (2 + \sqrt{x}) dx = 2x e^{\sqrt{x}} + C$ -
通解与特解
代入积分结果并整理:
$y = 2x + C e^{-\sqrt{x}}$
利用初始条件$y(1) = 3$,解得$C = e$,故特解为:
$y = 2x + e^{1 - \sqrt{x}}$
分析渐近线
当$x \to +\infty$时,指数项$e^{1 - \sqrt{x}} \to 0$,因此:
$y \approx 2x$
故曲线有一条斜渐近线$y = 2x$。