题目
下列各函数中可以作为某个随机变量的概率密度函数的是( )。A.f(x)= ) 2(1-|x|)|x|leqslant 1 0 .
下列各函数中可以作为某个随机变量的概率密度函数的是( )。
- A.
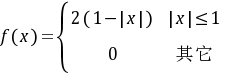
- B.
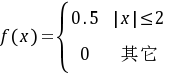
- C.
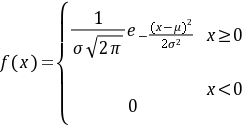
- D.
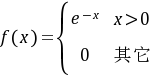
题目解答
答案
D
解析
概率密度函数必须满足两个条件:
- 非负性:对任意实数$x$,$f(x) \geq 0$;
- 归一性:$\int_{-\infty}^{+\infty} f(x) \, dx = 1$。
本题需逐一验证选项是否满足这两个条件。关键在于:
- 非负性:检查函数定义是否非负;
- 归一性:计算积分是否为1。
选项A
$f(x)= \begin{cases} 2(1-|x|) & |x| \leqslant 1 \\ 0 & \text{其他} \end{cases}$
- 非负性:当$|x| \leqslant 1$时,$1-|x| \geq 0$,故$2(1-|x|) \geq 0$,满足非负性。
- 归一性:计算积分:
$\int_{-1}^{1} 2(1-|x|) \, dx = 2 \int_{0}^{1} 2(1-x) \, dx = 4 \left[ x - \frac{x^2}{2} \right]_0^1 = 4 \cdot \frac{1}{2} = 2 \neq 1$
不满足归一性,排除。
选项B
$f(x)= \begin{cases} 0.5 & |x| \leqslant 2 \\ 0 & \text{其他} \end{cases}$
- 非负性:$0.5 \geq 0$,满足非负性。
- 归一性:计算积分:
$\int_{-2}^{2} 0.5 \, dx = 0.5 \cdot 4 = 2 \neq 1$
不满足归一性,排除。
选项C
$f(x)= \begin{cases} \dfrac{1}{0\sqrt{2\pi}} e^{-\frac{(x-a)^2}{2a^2}} & x \geqslant 0 \\ 0 & x < 0 \end{cases}$
- 非负性:分母为$0$,表达式无意义,函数本身不合法,排除。
选项D
$f(x)= \begin{cases} e^{-x} & x > 0 \\ 0 & \text{其他} \end{cases}$
- 非负性:$e^{-x} > 0$($x > 0$时),其他情况为$0$,满足非负性。
- 归一性:计算积分:
$\int_{0}^{+\infty} e^{-x} \, dx = 1$
满足归一性,正确。