题目
5.设二维离散型随机变量(X,Y)的联合分布律如下.-|||-2 3-|||-X-|||-1 dfrac (1)(6) dfrac (1)(9) dfrac (1)(18)-|||-2 dfrac (1)(3) α β-|||-问:α,β取什么值时X与Y相互独立?

题目解答
答案
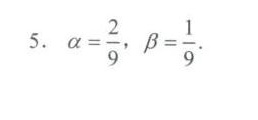
解析
考查要点:本题主要考查二维离散型随机变量的独立性条件,需要根据联合分布律确定参数α和β的值,使得X与Y相互独立。
解题核心思路:
- 独立性条件:X与Y独立当且仅当对所有i,j,有$P(X=x_i, Y=y_j) = P(X=x_i) \cdot P(Y=y_j)$。
- 边缘分布计算:先通过联合分布律计算X和Y的边缘分布。
- 方程联立求解:利用独立性条件建立方程,结合概率和为1的约束条件求解α和β。
破题关键点:
- 验证边缘分布的乘积是否等于联合概率,尤其注意未知参数对应的单元格。
- 利用概率和为1的隐含条件,确保解的合理性。
步骤1:确定X和Y的边缘分布
-
X的边缘分布:
- $P(X=1) = \dfrac{1}{6} + \dfrac{1}{9} + \dfrac{1}{18} = \dfrac{1}{3}$
- $P(X=2) = 1 - \dfrac{1}{3} = \dfrac{2}{3}$
-
Y的边缘分布(需结合未知参数):
- $P(Y=1) = \dfrac{1}{6} + \dfrac{1}{3} = \dfrac{1}{2}$
- $P(Y=2) = \dfrac{1}{9} + \alpha$
- $P(Y=3) = \dfrac{1}{18} + \beta$
步骤2:利用独立性条件建立方程
根据独立性条件$P(X=x_i, Y=y_j) = P(X=x_i) \cdot P(Y=y_j)$,对含未知参数的单元格列方程:
-
当$X=1, Y=2$时:
$\dfrac{1}{9} = \dfrac{1}{3} \cdot \left( \dfrac{1}{9} + \alpha \right) \implies \alpha = \dfrac{2}{9}$ -
当$X=1, Y=3$时:
$\dfrac{1}{18} = \dfrac{1}{3} \cdot \left( \dfrac{1}{18} + \beta \right) \implies \beta = \dfrac{1}{9}$
步骤3:验证概率和为1
所有概率之和应为1:
$\dfrac{1}{6} + \dfrac{1}{9} + \dfrac{1}{18} + \dfrac{1}{3} + \dfrac{2}{9} + \dfrac{1}{9} = 1$
验证通过,解合理。