题目
设电路由A,B,C三个元件组成,若元件A,B,C发生故障的概率分别是0.3,0.2,0.2,且各元件独立工作,试在以下情况下,求此电路发生故障的概率:(1)A,B,C三个元件串联(2)A,B,C三个元件并联(3)元件A与两个并联的元件B及C串联
设电路由A,B,C三个元件组成,若元件A,B,C发生故障的概率分别是0.3,0.2,0.2,且各元件独立工作,试在以下情况下,求此电路发生故障的概率:
(1)A,B,C三个元件串联
(2)A,B,C三个元件并联
(3)元件A与两个并联的元件B及C串联
题目解答
答案
解:记E为电路发生故障,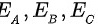 分别代表元件A,B,C发生故障
分别代表元件A,B,C发生故障
由题意可知,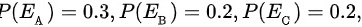
(1)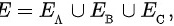
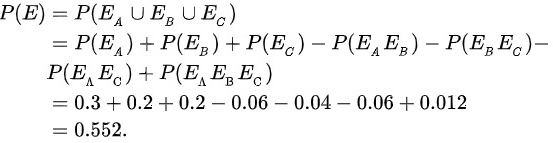
A,B,C三个元件串联的概率为0.552
(2)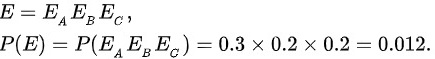
A,B,C三个元件并联的概率为0.012
(3)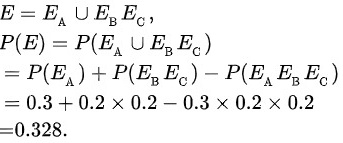
元件A与两个并联的元件B及C串联的概率为0.328
解析
考查要点:本题主要考查独立事件的概率计算,以及不同电路连接方式(串联、并联、混合连接)对应的故障概率分析。
解题核心思路:
- 串联电路:电路故障当且仅当至少有一个元件故障。等价于所有元件正常工作的概率的补集。
- 并联电路:电路故障当且仅当所有元件同时故障,直接相乘各元件故障概率。
- 混合连接:分解为串联和并联的组合,先计算并联部分的正常工作概率,再结合串联部分计算整体故障概率。
破题关键点:
- 独立事件性质:各元件故障相互独立,概率可直接相乘。
- 电路逻辑转换:串联对应“至少一个故障”,并联对应“全部故障”,混合连接需分步分析。
第(1)题:串联电路
电路故障条件
串联电路中,只要有一个元件故障,整个电路就故障。因此,电路正常工作的概率为各元件正常概率的乘积:
$P(\text{正常}) = P(A\text{正常}) \cdot P(B\text{正常}) \cdot P(C\text{正常}) = 0.7 \cdot 0.8 \cdot 0.8 = 0.448$
计算电路故障概率
$P(\text{故障}) = 1 - P(\text{正常}) = 1 - 0.448 = 0.552$
第(2)题:并联电路
电路故障条件
并联电路中,所有元件必须同时故障,因此:
$P(\text{故障}) = P(A\text{故障}) \cdot P(B\text{故障}) \cdot P(C\text{故障}) = 0.3 \cdot 0.2 \cdot 0.2 = 0.012$
第(3)题:混合连接(A与B、C并联串联)
分解电路结构
电路由A与(B并联C)串联组成,需分两步计算:
- B与C并联部分的故障概率:
$P(B\text{和}C\text{同时故障}) = P(B\text{故障}) \cdot P(C\text{故障}) = 0.2 \cdot 0.2 = 0.04$ - 整体电路故障条件:
- A故障,或
- A正常但B和C同时故障:
$P(\text{故障}) = P(A\text{故障}) + P(A\text{正常}) \cdot P(B\text{和}C\text{同时故障}) = 0.3 + 0.7 \cdot 0.04 = 0.328$