题目
, . . . .-|||-10.已知曲线 =a(x)^3+b(x)^2 的一个拐点为(1,3),求a ,b的值.
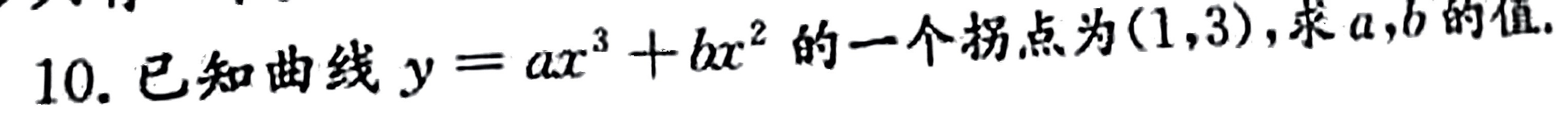
题目解答
答案
y'=3ax²+2bx
y''=6ax+2b
因为(1,3)是拐点
所以0=6a+2b
3=a+b
解得a=-3/2,b=9/2
解析
步骤 1:求一阶导数
对给定的函数 $y=a{x}^{3}+b{x}^{2}$ 求一阶导数,得到 $y'=3ax^2+2bx$。
步骤 2:求二阶导数
对一阶导数 $y'=3ax^2+2bx$ 求导,得到 $y''=6ax+2b$。
步骤 3:利用拐点条件
由于(1,3)是曲线的拐点,所以该点处的二阶导数为0,即 $y''(1)=0$。将x=1代入二阶导数表达式,得到 $6a+2b=0$。
步骤 4:利用点在曲线上的条件
由于点(1,3)在曲线上,所以将x=1,y=3代入原函数表达式,得到 $3=a+b$。
步骤 5:解方程组
联立步骤3和步骤4得到的方程,即 $6a+2b=0$ 和 $3=a+b$,解这个方程组得到a和b的值。
对给定的函数 $y=a{x}^{3}+b{x}^{2}$ 求一阶导数,得到 $y'=3ax^2+2bx$。
步骤 2:求二阶导数
对一阶导数 $y'=3ax^2+2bx$ 求导,得到 $y''=6ax+2b$。
步骤 3:利用拐点条件
由于(1,3)是曲线的拐点,所以该点处的二阶导数为0,即 $y''(1)=0$。将x=1代入二阶导数表达式,得到 $6a+2b=0$。
步骤 4:利用点在曲线上的条件
由于点(1,3)在曲线上,所以将x=1,y=3代入原函数表达式,得到 $3=a+b$。
步骤 5:解方程组
联立步骤3和步骤4得到的方程,即 $6a+2b=0$ 和 $3=a+b$,解这个方程组得到a和b的值。