题目
已知点A(1,2),B(a,3), |AB|=sqrt (10),则A(1,2),B(a,3), |AB|=sqrt (10).A.-2 B.4 C.-2或4 D.2
已知点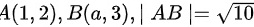 ,则
,则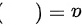 .
.
A.-2
B.4
C.-2或4
D.2
题目解答
答案
根据题意知,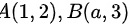 ,由两点间距离公式可得
,由两点间距离公式可得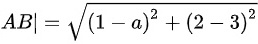 ,则
,则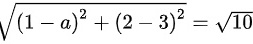 ,即
,即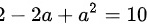 ,解得
,解得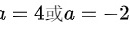 .
.
故选:C.
解析
步骤 1:应用两点间距离公式
根据题意,点A(1,2)和点B(a,3)之间的距离$|AB|$等于$\sqrt{10}$。根据两点间距离公式,$|AB|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$,代入点A和点B的坐标,得到$|AB|=\sqrt{(a-1)^2+(3-2)^2}$。
步骤 2:建立方程
将$|AB|=\sqrt{10}$代入上一步得到的公式中,得到$\sqrt{(a-1)^2+1^2}=\sqrt{10}$。进一步简化得到$(a-1)^2+1=10$。
步骤 3:求解方程
从$(a-1)^2+1=10$中解出$a$,得到$(a-1)^2=9$。解这个方程得到$a-1=3$或$a-1=-3$,从而得到$a=4$或$a=-2$。
根据题意,点A(1,2)和点B(a,3)之间的距离$|AB|$等于$\sqrt{10}$。根据两点间距离公式,$|AB|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$,代入点A和点B的坐标,得到$|AB|=\sqrt{(a-1)^2+(3-2)^2}$。
步骤 2:建立方程
将$|AB|=\sqrt{10}$代入上一步得到的公式中,得到$\sqrt{(a-1)^2+1^2}=\sqrt{10}$。进一步简化得到$(a-1)^2+1=10$。
步骤 3:求解方程
从$(a-1)^2+1=10$中解出$a$,得到$(a-1)^2=9$。解这个方程得到$a-1=3$或$a-1=-3$,从而得到$a=4$或$a=-2$。