题目
下列公式错误的是A.int dfrac (1)({a)^2+(x)^2}dx=arctan dfrac (x)(a)+C,(aneq 0)B.int dfrac (1)({a)^2+(x)^2}dx=arctan dfrac (x)(a)+C,(aneq 0)C.int dfrac (1)({a)^2+(x)^2}dx=arctan dfrac (x)(a)+C,(aneq 0)D.int dfrac (1)({a)^2+(x)^2}dx=arctan dfrac (x)(a)+C,(aneq 0)
下列公式错误的是
A.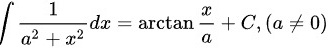
B.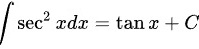
C.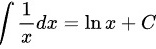
D.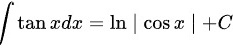
题目解答
答案
解:
A选项,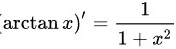 ;
;
B选项,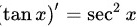 ;
;
C选项,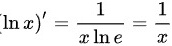 ;
;
D选项,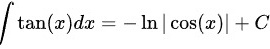 .
.
∴本题选择D。
解析
步骤 1:分析选项A
根据积分公式,$\int \dfrac {1}{{a}^{2}+{x}^{2}}dx=\dfrac {1}{a}\arctan \dfrac {x}{a}+C$,其中$a\neq 0$。因此,选项A是正确的。
步骤 2:分析选项B
根据微分公式,$(\tan x)'={\sec }^{2}x$,因此,$\int {\sec }^{2}xdx=\tan x+C$。所以,选项B是正确的。
步骤 3:分析选项C
根据积分公式,$\int \dfrac {1}{x}dx=\ln |x|+C$。因此,选项C是正确的。
步骤 4:分析选项D
根据积分公式,$\int \tan xdx=-\ln |\cos x|+C$。因此,选项D是错误的。
根据积分公式,$\int \dfrac {1}{{a}^{2}+{x}^{2}}dx=\dfrac {1}{a}\arctan \dfrac {x}{a}+C$,其中$a\neq 0$。因此,选项A是正确的。
步骤 2:分析选项B
根据微分公式,$(\tan x)'={\sec }^{2}x$,因此,$\int {\sec }^{2}xdx=\tan x+C$。所以,选项B是正确的。
步骤 3:分析选项C
根据积分公式,$\int \dfrac {1}{x}dx=\ln |x|+C$。因此,选项C是正确的。
步骤 4:分析选项D
根据积分公式,$\int \tan xdx=-\ln |\cos x|+C$。因此,选项D是错误的。