题目
(3)设曲线L是圆周 ((x-1))^2+(y)^2=(R)^2 沿逆时针方向一周,则曲线积分-|||-dfrac ((x-1)dy-ydx)({(x-1))^2+(y)^2}= () ;-|||-(A)2π· (B) -2pi (C)0. (D)π,
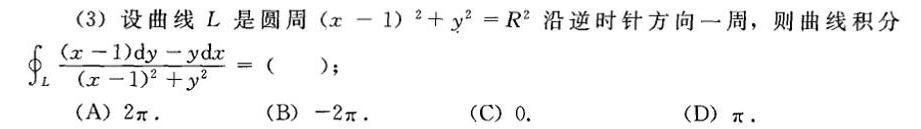
题目解答
答案
解析
步骤 1:参数化曲线
将圆周参数化为 $x=1+R\cos\theta$ 和 $y=R\sin\theta$,其中 $\theta$ 从 $0$ 到 $2\pi$。
步骤 2:计算微分
计算 $dx$ 和 $dy$,得到 $dx=-R\sin\theta d\theta$ 和 $dy=R\cos\theta d\theta$。
步骤 3:代入并简化
将 $x$,$y$,$dx$ 和 $dy$ 代入曲线积分中,得到
$$\int_{L} \frac{(x-1)dy-ydx}{(x-1)^2+y^2} = \int_{0}^{2\pi} \frac{R^2\cos^2\theta+R^2\sin^2\theta}{R^2} d\theta = \int_{0}^{2\pi} d\theta = 2\pi$$
将圆周参数化为 $x=1+R\cos\theta$ 和 $y=R\sin\theta$,其中 $\theta$ 从 $0$ 到 $2\pi$。
步骤 2:计算微分
计算 $dx$ 和 $dy$,得到 $dx=-R\sin\theta d\theta$ 和 $dy=R\cos\theta d\theta$。
步骤 3:代入并简化
将 $x$,$y$,$dx$ 和 $dy$ 代入曲线积分中,得到
$$\int_{L} \frac{(x-1)dy-ydx}{(x-1)^2+y^2} = \int_{0}^{2\pi} \frac{R^2\cos^2\theta+R^2\sin^2\theta}{R^2} d\theta = \int_{0}^{2\pi} d\theta = 2\pi$$