题目
31.设随机变量(X,Y)具有概率密度-|||-f(x,y)= ) 1, |y|lt x, 0lt xlt 1 0, .-|||-求E(X),E(Y ),Cov(X,Y).
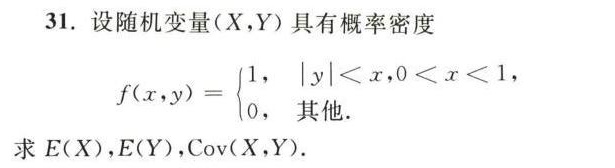
题目解答
答案

解析
步骤 1:计算E(X)
根据概率密度函数f(x,y)的定义,E(X)的计算公式为:
$$E(X) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x f(x,y) \, dx \, dy$$
由于f(x,y)只在区域$G: \{ (x,y) | |y| < x, 0 < x < 1 \}$上不等于零,因此:
$$E(X) = \iint_{G} x \, dx \, dy$$
将区域G的边界代入,得到:
$$E(X) = \int_{0}^{1} \int_{-x}^{x} x \, dy \, dx$$
步骤 2:计算E(Y)
根据概率密度函数f(x,y)的定义,E(Y)的计算公式为:
$$E(Y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} y f(x,y) \, dx \, dy$$
由于f(x,y)只在区域$G: \{ (x,y) | |y| < x, 0 < x < 1 \}$上不等于零,因此:
$$E(Y) = \iint_{G} y \, dx \, dy$$
将区域G的边界代入,得到:
$$E(Y) = \int_{0}^{1} \int_{-x}^{x} y \, dy \, dx$$
步骤 3:计算Cov(X,Y)
根据协方差的定义,Cov(X,Y)的计算公式为:
$$Cov(X,Y) = E(XY) - E(X)E(Y)$$
其中,$E(XY)$的计算公式为:
$$E(XY) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} xy f(x,y) \, dx \, dy$$
由于f(x,y)只在区域$G: \{ (x,y) | |y| < x, 0 < x < 1 \}$上不等于零,因此:
$$E(XY) = \iint_{G} xy \, dx \, dy$$
将区域G的边界代入,得到:
$$E(XY) = \int_{0}^{1} \int_{-x}^{x} xy \, dy \, dx$$
根据概率密度函数f(x,y)的定义,E(X)的计算公式为:
$$E(X) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x f(x,y) \, dx \, dy$$
由于f(x,y)只在区域$G: \{ (x,y) | |y| < x, 0 < x < 1 \}$上不等于零,因此:
$$E(X) = \iint_{G} x \, dx \, dy$$
将区域G的边界代入,得到:
$$E(X) = \int_{0}^{1} \int_{-x}^{x} x \, dy \, dx$$
步骤 2:计算E(Y)
根据概率密度函数f(x,y)的定义,E(Y)的计算公式为:
$$E(Y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} y f(x,y) \, dx \, dy$$
由于f(x,y)只在区域$G: \{ (x,y) | |y| < x, 0 < x < 1 \}$上不等于零,因此:
$$E(Y) = \iint_{G} y \, dx \, dy$$
将区域G的边界代入,得到:
$$E(Y) = \int_{0}^{1} \int_{-x}^{x} y \, dy \, dx$$
步骤 3:计算Cov(X,Y)
根据协方差的定义,Cov(X,Y)的计算公式为:
$$Cov(X,Y) = E(XY) - E(X)E(Y)$$
其中,$E(XY)$的计算公式为:
$$E(XY) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} xy f(x,y) \, dx \, dy$$
由于f(x,y)只在区域$G: \{ (x,y) | |y| < x, 0 < x < 1 \}$上不等于零,因此:
$$E(XY) = \iint_{G} xy \, dx \, dy$$
将区域G的边界代入,得到:
$$E(XY) = \int_{0}^{1} \int_{-x}^{x} xy \, dy \, dx$$