题目
已知2 0 0-|||-0 1 3-|||-0 2 5,矩阵2 0 0-|||-0 1 3-|||-0 2 5满足2 0 0-|||-0 1 3-|||-0 2 5,其中2 0 0-|||-0 1 3-|||-0 2 5为2 0 0-|||-0 1 3-|||-0 2 5的伴随矩阵,则2 0 0-|||-0 1 3-|||-0 2 5( ).2 0 0-|||-0 1 3-|||-0 2 52 0 0-|||-0 1 3-|||-0 2 52 0 0-|||-0 1 3-|||-0 2 52 0 0-|||-0 1 3-|||-0 2 5
已知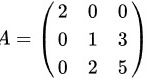 ,矩阵
,矩阵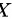 满足
满足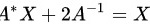 ,其中
,其中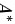 为
为 的伴随矩阵,则
的伴随矩阵,则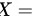 ( ).
( ).
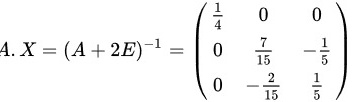
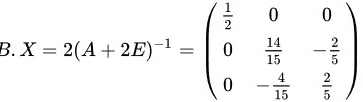
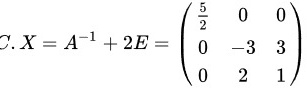
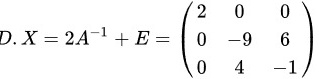
题目解答
答案
将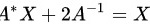 两边同时左乘矩阵
两边同时左乘矩阵 ,得到:
,得到: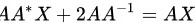
∴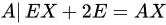
由按行展开的行列式计算公式可知: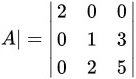

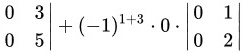
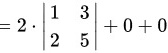
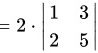
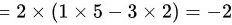
故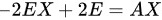
∴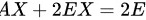
∴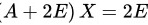
由矩阵的数乘运算可知:
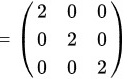
由矩阵的加法运算可知: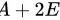

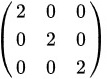


将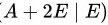 进行如下的行初等变换:
进行如下的行初等变换:
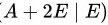
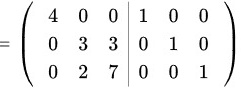
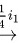

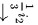

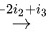
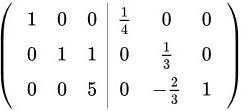
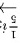

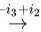
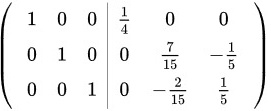
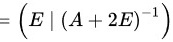
故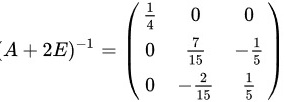
将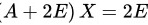 两边同时右乘矩阵
两边同时右乘矩阵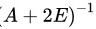 ,得到:
,得到: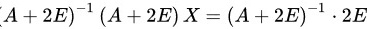
∴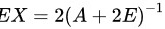
∴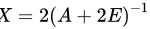
故由矩阵的数乘运算可知: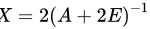
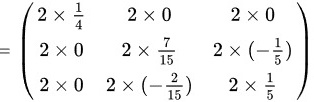
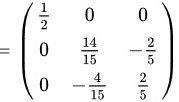
故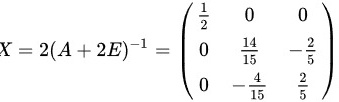
故答案是: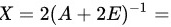
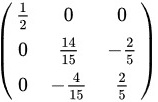 ,选
,选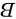
解析
步骤 1:将给定的矩阵方程两边同时左乘矩阵A
将${A}^{*}X+2{A}^{-1}=X$两边同时左乘矩阵A,得到:${AA}^{*}X+2{AA}^{-1}=AX$。
步骤 2:利用伴随矩阵的性质简化方程
由伴随矩阵的性质,我们知道$AA^* = |A|E$,其中$|A|$是矩阵A的行列式,E是单位矩阵。因此,方程变为$|A|EX+2E=AX$。
步骤 3:计算矩阵A的行列式
由按行展开的行列式计算公式可知:$|A|=2\times (1\times 5-3\times 2)=-2$。
步骤 4:代入行列式的值并简化方程
将$|A|=-2$代入方程,得到$-2EX+2E=AX$,即$AX+2EX=2E$。
步骤 5:将方程变形为$(A+2E)X=2E$
将方程变形为$(A+2E)X=2E$。
步骤 6:计算矩阵$(A+2E)$的逆矩阵
将$(A+2E|E)$进行如下的行初等变换:$(A+2E|E)$1 $\dfrac {t}{1}$$\dfrac {1}{3}{z}_{2}$$-2{i}_{2}+{i}_{3}$$\dfrac {1}{5}$:$-\dot {3}3+\dot {2}2$$=(E|{(A+2E)}^{-1})$。
步骤 7:求解矩阵X
将$(A+2E)X=2E$两边同时右乘矩阵${(A+2E)}^{-1}$,得到:${A+2E)}^{-1}(A+2E)X={(A+2E)}^{-1}\cdot 2E$,即$X=2{(A+2E)}^{-1}$。
将${A}^{*}X+2{A}^{-1}=X$两边同时左乘矩阵A,得到:${AA}^{*}X+2{AA}^{-1}=AX$。
步骤 2:利用伴随矩阵的性质简化方程
由伴随矩阵的性质,我们知道$AA^* = |A|E$,其中$|A|$是矩阵A的行列式,E是单位矩阵。因此,方程变为$|A|EX+2E=AX$。
步骤 3:计算矩阵A的行列式
由按行展开的行列式计算公式可知:$|A|=2\times (1\times 5-3\times 2)=-2$。
步骤 4:代入行列式的值并简化方程
将$|A|=-2$代入方程,得到$-2EX+2E=AX$,即$AX+2EX=2E$。
步骤 5:将方程变形为$(A+2E)X=2E$
将方程变形为$(A+2E)X=2E$。
步骤 6:计算矩阵$(A+2E)$的逆矩阵
将$(A+2E|E)$进行如下的行初等变换:$(A+2E|E)$1 $\dfrac {t}{1}$$\dfrac {1}{3}{z}_{2}$$-2{i}_{2}+{i}_{3}$$\dfrac {1}{5}$:$-\dot {3}3+\dot {2}2$$=(E|{(A+2E)}^{-1})$。
步骤 7:求解矩阵X
将$(A+2E)X=2E$两边同时右乘矩阵${(A+2E)}^{-1}$,得到:${A+2E)}^{-1}(A+2E)X={(A+2E)}^{-1}\cdot 2E$,即$X=2{(A+2E)}^{-1}$。