题目
化简表达式dfrac ({x)^3-3(x)^2+2x}({x)^2-4}
化简表达式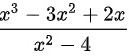
题目解答
答案
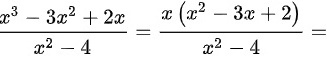
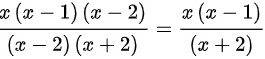
故本题答案为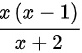
解析
考查要点:本题主要考查分式的化简,涉及因式分解和约分的基本方法。
解题思路:
- 分解分子和分母的因式:分子提取公因式后进一步分解二次多项式,分母利用平方差公式分解。
- 约分:找到分子和分母的公共因式并约去,注意分式成立的条件(分母不为零)。
关键点:正确分解因式是约分的前提,需注意分解的彻底性。
步骤1:分解分子
原式分子为 $x^3 - 3x^2 + 2x$,首先提取公因式 $x$:
$x^3 - 3x^2 + 2x = x(x^2 - 3x + 2)$
进一步分解二次多项式 $x^2 - 3x + 2$,寻找两数乘积为 $2$ 且和为 $-3$,得:
$x^2 - 3x + 2 = (x - 1)(x - 2)$
因此,分子分解为:
$x(x - 1)(x - 2)$
步骤2:分解分母
分母为 $x^2 - 4$,利用平方差公式分解:
$x^2 - 4 = (x - 2)(x + 2)$
步骤3:约分
将分子和分母的公共因式 $(x - 2)$ 约去,注意 $x \neq 2$:
$\frac{x(x - 1)(x - 2)}{(x - 2)(x + 2)} = \frac{x(x - 1)}{x + 2}$