题目

已知二维随机变量的联合分布律为：，问：（1）X和Y是否相互独立；（2）X与Y是否不相关，并求.

已知二维随机变量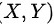 $(X,Y)$ 的联合分布律为： $\begin{pmatrix} X/Y&1&2 \newline 1&0.35&0.35\newline 2&0.15&0.15 \end{pmatrix}$ ，问：

（1）X和Y是否相互独立；

（2）X与Y是否不相关，并求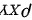 $\rho_{XY}$ .

题目解答

答案

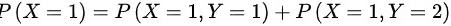
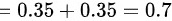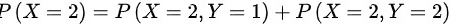
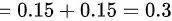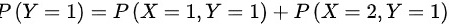
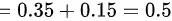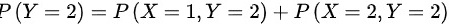
（1）X的边缘分布律为 $P\left(X=1\right)=P\left(X=1,Y=1\right)+P\left(X=1,Y=2\right)$ $=0.35+0.35=0.7$ ， $P\left(X=2\right)=P\left(X=2,Y=1\right)+P\left(X=2,Y=2\right)$ $=0.15+0.15=0.3$ ，Y的边缘分布律为 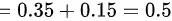$P\left(Y=1\right)=P\left(X=1,Y=1\right)+P\left(X=2,Y=1\right)$ $=0.35+0.15=0.5$ ， $P\left(Y=2\right)=P\left(X=1,Y=2\right)+P\left(X=2,Y=2\right)$ $=0.35+0.15=0.5$ ，则 $P\left(X=1\right)P\left(Y=1\right)=0.7\times0.5=0.35=P\left(X=1,Y=1\right)$ ， $P\left(X=1\right)P\left(Y=2\right)=0.7\times0.5=0.35=P\left(X=1,Y=2\right)$ ， $P\left(X=2\right)P\left(Y=1\right)=0.3\times0.5=0.15=P\left(X=2,Y=1\right)$ ， $P\left(X=2\right)P\left(Y=2\right)=0.3\times0.5=0.15=P\left(X=2,Y=2\right)$ ，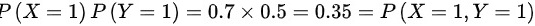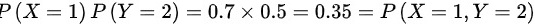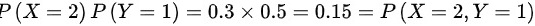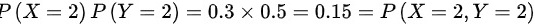即X与Y边缘分布律的乘积等于联合分布律，则X与Y相互独立；（2）相互独立随机变量一定不相关，则X与Y的相关系数为 $\rho_{XY}=0$ .

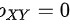解析

步骤 1：计算边缘分布律
- X的边缘分布律为$P(X=1)=P(X=1,Y=1)+P(X=1,Y=2)$=0.35+0.15=0.5，$P(X=2)=P(X=2,Y=1)+P(X=2,Y=2)$=0.35+0.15=0.5。
- Y的边缘分布律为$P(Y=1)=P(X=1,Y=1)+P(X=2,Y=1)$=0.35+0.35=0.7，$P(Y=2)=P(X=1,Y=2)+P(X=2,Y=2)$=0.15+0.15=0.3。

步骤 2：判断X和Y是否相互独立
- 检查$P(X=1,Y=1)=P(X=1)P(Y=1)$，即0.35=0.5*0.7=0.35，成立。
- 检查$P(X=1,Y=2)=P(X=1)P(Y=2)$，即0.15=0.5*0.3=0.15，成立。
- 检查$P(X=2,Y=1)=P(X=2)P(Y=1)$，即0.35=0.5*0.7=0.35，成立。
- 检查$P(X=2,Y=2)=P(X=2)P(Y=2)$，即0.15=0.5*0.3=0.15，成立。
- 因此，X和Y相互独立。

步骤 3：判断X与Y是否不相关
- 由于X和Y相互独立，所以它们一定不相关。
- 计算$1\times {0}^{2}$，即$1\times 0=0$。