题目
求指导本题解题过程,谢谢您!5.设a1,a2,β1,β2是3维列向量, =((a)_(1),(a)_(2),(beta )_(1)) , =((a)_(1),2(a)_(2),(beta )_(2)), 且 |A|=1,-|||-|B|=2, 则 |A+B|= __ _。
求指导本题解题过程,谢谢您!
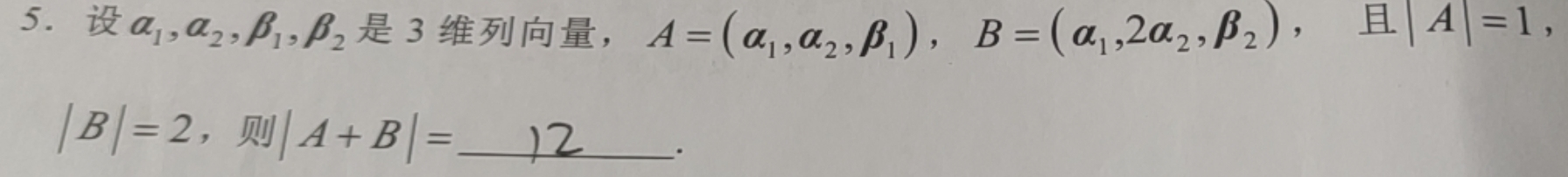
题目解答
答案

解析
本题主要考察矩阵行列式的性质,包括矩阵加法运算、数乘运算对行列式的影响,以及行列式的拆分法则。
步骤1:计算矩阵$A+B$
已知矩阵$A=(a_1,a_2,\beta_1)$,$B=(a_1,2a_2,\beta_2)$,矩阵加法是对应列向量相加,因此:
$A+B=(a_1+a_1,\ a_2+2a_2,\ \beta_1+\beta_2)=(2a_1,\ 3a_2,\ \beta_1+\beta_2)$
步骤2:拆分$\beta_1+\beta_2$,利用行列式可加性
行列式的性质:若矩阵某一列是两个向量之和,则行列式可拆分为两个行列式之和:
$|A+B|=\begin{vmatrix}2a_1 & 3a_2 & \beta_1+\beta_2\end{vmatrix}=\begin{vmatrix}2a_1 & 3a_2 & \beta_1\end{vmatrix}+\begin{vmatrix}2a_1 & 3a_2 & \beta_2\end{vmatrix}$
步骤3:计算第一个行列式$\begin{vmatrix}2a_1 & 3a_2 & \beta_1\end{vmatrix}$
行列式性质:某一列数乘$k$,行列式值变为$k$倍原行列式;多列数乘时,倍数相乘:
- 第一列$a_1$数乘$2$,行列式变为$2\begin{vmatrix}a_1 & 3a_2 & \beta_1\end{vmatrix}$
- 第二列$a_2$数乘$3$,行列式变为$2\times3\begin{vmatrix}a_1 & a_2 & \beta_1\end{vmatrix}=6|A|$
已知$|A|=1$,故该行列式$=6\times1=6$。
步骤4:计算第二个行列式$\begin{vmatrix}2a_1 & 3a_2 & \beta_2\end{vmatrix}$
同理:
- 第一列数乘$2$,第二列数乘$3$,行列式变为$2\times3\begin{vmatrix}a_1 & a_2 & \beta_2\end{vmatrix}$
注意$\begin{vmatrix}a_1 & a_2 & \beta_2\end{vmatrix}$与$|B|$的关系:$|B|=\begin{vmatrix}a_1 & 2a_2 & \beta_2\end{vmatrix}=2\begin{vmatrix}a_1 & a_2 & \beta_2\end{vmatrix}$,故$\begin{vmatrix}a_1 & a_2 & \beta_2\end{vmatrix}=\frac{1}{2}|B|$
代入得:$6\times\frac{1}{2}|B|=3|B|$,已知$|B|=2$,故该行列式$=3\times2=6$。
步骤5:求和得$|A+B|$
$|A+B|=6+6=12$