题目
已知(x)=sin (3x+dfrac (pi )(4)),则(x)=sin (3x+dfrac (pi )(4))= ( ) A . -3 B . 3 C . 0 D . -1
已知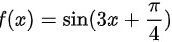 ,则
,则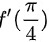 = ( )
= ( )
A . -3
B . 3
C . 0
D . -1
题目解答
答案
解:∵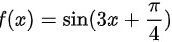
∴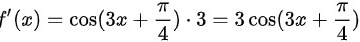
∴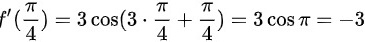
故答案为:A
解析
步骤 1:求导
根据复合函数的求导法则,对$f(x)=\sin (3x+\dfrac {\pi }{4})$求导,得到$f'(x)=\cos (3x+\dfrac {\pi }{4})\cdot 3$。
步骤 2:代入$x=\dfrac {\pi }{4}$
将$x=\dfrac {\pi }{4}$代入$f'(x)$中,得到$f'(\dfrac {\pi }{4})=3\cos (3\cdot \dfrac {\pi }{4}+\dfrac {\pi }{4})$。
步骤 3:计算$f'(\dfrac {\pi }{4})$
计算$f'(\dfrac {\pi }{4})=3\cos (\dfrac {3\pi }{4}+\dfrac {\pi }{4})=3\cos \pi =-3$。
根据复合函数的求导法则,对$f(x)=\sin (3x+\dfrac {\pi }{4})$求导,得到$f'(x)=\cos (3x+\dfrac {\pi }{4})\cdot 3$。
步骤 2:代入$x=\dfrac {\pi }{4}$
将$x=\dfrac {\pi }{4}$代入$f'(x)$中,得到$f'(\dfrac {\pi }{4})=3\cos (3\cdot \dfrac {\pi }{4}+\dfrac {\pi }{4})$。
步骤 3:计算$f'(\dfrac {\pi }{4})$
计算$f'(\dfrac {\pi }{4})=3\cos (\dfrac {3\pi }{4}+\dfrac {\pi }{4})=3\cos \pi =-3$。