题目
若行列式1 1 1-|||-a b c neq 0-|||-a^2 b^2 c^2,则( )A.1 1 1-|||-a b c neq 0-|||-a^2 b^2 c^2B.1 1 1-|||-a b c neq 0-|||-a^2 b^2 c^2不全相等C.1 1 1-|||-a b c neq 0-|||-a^2 b^2 c^2全不相等D.1 1 1-|||-a b c neq 0-|||-a^2 b^2 c^2
若行列式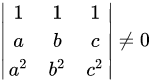 ,则( )
,则( )
A.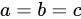
B.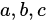 不全相等
不全相等
C.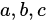 全不相等
全不相等
D.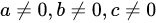
题目解答
答案
因为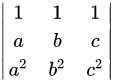
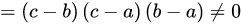
所以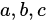 全不相等
全不相等
所以答案是C
解析
本题考查行列式的性质与因式分解。关键点在于识别行列式的结构,利用范德蒙德行列式的结论,或通过展开式分解因式,从而判断行列式不为零的条件。核心思路是将行列式展开为$(c-b)(c-a)(b-a)$,并分析各因子不为零的条件。
假设题目中的行列式为范德蒙德行列式:
$\begin{vmatrix}1 & a & a^2 \\1 & b & b^2 \\1 & c & c^2\end{vmatrix}$
范德蒙德行列式的展开结果为:
$(c-b)(c-a)(b-a)$
分析条件:
- 若行列式值$\neq 0$,则$(c-b)(c-a)(b-a) \neq 0$。
- 这要求每个因子均$\neq 0$,即:
- $c \neq b$,
- $c \neq a$,
- $b \neq a$。
- 因此,a、b、c两两不相等,即全不相等。