题目
设随机变量X服从参数为4的泊松分布，=(x)a，=(x)a，则=(x)a.A.133B.61C.-1D.71
设随机变量X服从参数为4的泊松分布，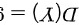
，
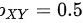，则
.
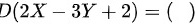A.133
B.61
C.-1
D.71
题目解答
答案
随机变量X服从参数为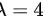
的泊松分布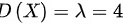，则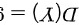
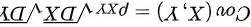
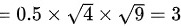，则，
，则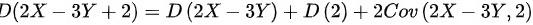
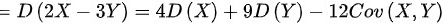
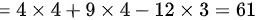，因此选择B。
解析
步骤 1：确定随机变量X的方差
随机变量X服从参数为4的泊松分布，因此其方差$D(X)=\lambda=4$。
步骤 2：确定随机变量Y的方差
由于${q}^{*}0=\lambda {x}_{0}$，可以推断出随机变量Y的方差$D(Y)=9$。
步骤 3：计算协方差
根据$=(x)a$，可以得出$Coo(X,Y)=\rho XY\sqrt {DX}\sqrt {DY}=0.5\times \sqrt {4}\times \sqrt {9}=3$。
步骤 4：计算D(2X-3Y+2)
$D(2X-3Y+2)=D(2X-3Y)+D(2)+2C\tan (2X-3Y,2)$
$D(2X-3Y)=4D(X)+9D(Y)-12Cou(X,Y)$
$=4\times 4+9\times 4-12\times 3=61$。
随机变量X服从参数为4的泊松分布，因此其方差$D(X)=\lambda=4$。
步骤 2：确定随机变量Y的方差
由于${q}^{*}0=\lambda {x}_{0}$，可以推断出随机变量Y的方差$D(Y)=9$。
步骤 3：计算协方差
根据$=(x)a$，可以得出$Coo(X,Y)=\rho XY\sqrt {DX}\sqrt {DY}=0.5\times \sqrt {4}\times \sqrt {9}=3$。
步骤 4：计算D(2X-3Y+2)
$D(2X-3Y+2)=D(2X-3Y)+D(2)+2C\tan (2X-3Y,2)$
$D(2X-3Y)=4D(X)+9D(Y)-12Cou(X,Y)$
$=4\times 4+9\times 4-12\times 3=61$。