题目
12.设随机变量X的密度函数为-|||-p(x)= ) 1-|x|,-1leqslant xleqslant 1 0, .-|||-试求X的分布函数.
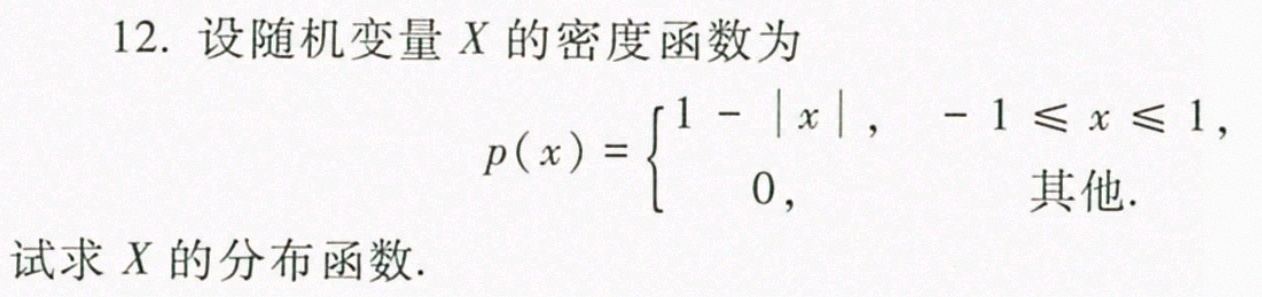
题目解答
答案

解析
考查要点:本题主要考查连续型随机变量分布函数的求解方法,重点在于理解密度函数的分段特性,并正确进行分段积分。
解题核心思路:
- 分段讨论:根据密度函数$p(x)$的定义域,将实数轴划分为四个区间:$x < -1$,$-1 \leq x < 0$,$0 \leq x < 1$,$x \geq 1$。
- 积分计算:在每个区间内,根据密度函数的具体表达式计算分布函数$F(x) = \int_{-\infty}^x p(t) \, dt$。
- 连续性验证:确保分布函数在分段点处连续。
破题关键点:
- 密度函数分段形式:在区间$[-1,0)$,$p(x)=1+x$;在区间$[0,1)$,$p(x)=1-x$。
- 积分区间简化:当$x$在某一区间时,只需对密度函数非零的部分积分。
当 $x < -1$ 时
密度函数$p(x)=0$,因此:
$F(x) = \int_{-\infty}^x 0 \, dt = 0.$
当 $-1 \leq x < 0$ 时
密度函数$p(x)=1+x$,积分区间为$[-1, x]$:
$\begin{aligned}F(x) &= \int_{-1}^x (1+t) \, dt \\&= \left[ t + \frac{t^2}{2} \right]_{-1}^x \\&= \left( x + \frac{x^2}{2} \right) - \left( -1 + \frac{1}{2} \right) \\&= \frac{x^2}{2} + x + \frac{1}{2}.\end{aligned}$
当 $0 \leq x < 1$ 时
需分两段积分:
- 从$-1$到$0$:
$\int_{-1}^0 (1+t) \, dt = \left[ t + \frac{t^2}{2} \right]_{-1}^0 = \frac{1}{2}.$ - 从$0$到$x$:
$\int_0^x (1-t) \, dt = \left[ t - \frac{t^2}{2} \right]_0^x = x - \frac{x^2}{2}.$
总和为:
$F(x) = \frac{1}{2} + x - \frac{x^2}{2} = -\frac{x^2}{2} + x + \frac{1}{2}.$
当 $x \geq 1$ 时
密度函数积分覆盖整个非零区域:
$F(x) = \int_{-1}^1 (1-|t|) \, dt = 1.$