x -1 0 0-|||-0 x -1 0-|||-0 0 x -1 =a3x ^3+a 2x^2+a1x+a 0.-|||-a0 a1 a2 a3
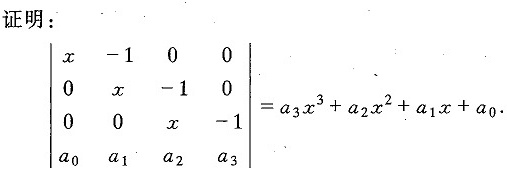
题目解答
答案

解析
考查要点:本题主要考查行列式的展开方法,特别是利用代数余子式展开计算四阶行列式,并验证其等于给定的三次多项式。
解题核心思路:
- 选择展开方式:优先选择元素较多或结构简单的行/列展开,简化计算。本题中,最后一行有三个非零元素(a0, a1, a2, a3),适合展开。
- 代数余子式计算:对每个元素对应的余子式进行递归展开,注意符号因子的计算。
- 归纳结果:将所有展开项相加,整理后得到目标多项式。
破题关键点:
- 正确识别行列式结构:前三行为上三角矩阵,最后一行打破结构。
- 符号因子的处理:代数余子式的符号由位置决定,需准确计算。
方法一:按最后一行展开
行列式为:
$D = \begin{vmatrix}x & -1 & 0 & 0 \\0 & x & -1 & 0 \\0 & 0 & x & -1 \\a_0 & a_1 & a_2 & a_3\end{vmatrix}$
按最后一行展开,得:
$D = a_0 A_{41} + a_1 A_{42} + a_2 A_{43} + a_3 A_{44}$
计算代数余子式
-
$A_{41}$(去掉第4行第1列):
$A_{41} = (-1)^{4+1} \begin{vmatrix}-1 & 0 & 0 \\x & -1 & 0 \\0 & x & -1\end{vmatrix} = (-1) \cdot (-1)^3 = 1$ -
$A_{42}$(去掉第4行第2列):
$A_{42} = (-1)^{4+2} \begin{vmatrix}x & 0 & 0 \\0 & -1 & 0 \\0 & x & -1\end{vmatrix} = 1 \cdot x = x$ -
$A_{43}$(去掉第4行第3列):
$A_{43} = (-1)^{4+3} \begin{vmatrix}x & -1 & 0 \\0 & x & 0 \\0 & 0 & -1\end{vmatrix} = (-1) \cdot (-x^2) = x^2$ -
$A_{44}$(去掉第4行第4列):
$A_{44} = (-1)^{4+4} \begin{vmatrix}x & -1 & 0 \\0 & x & -1 \\0 & 0 & x\end{vmatrix} = 1 \cdot x^3 = x^3$
整理结果
$D = a_0 \cdot 1 + a_1 \cdot x + a_2 \cdot x^2 + a_3 \cdot x^3 = a_3 x^3 + a_2 x^2 + a_1 x + a_0$