题目
【题文】lim _(narrow infty )dfrac ({2)^n+1+(3)^n+1}({2)^n+(3)^n}=________.
【题文】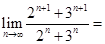
________.
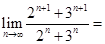________.题目解答
答案
【答案】3
解析
步骤 1：提取公因式
观察分子和分母，可以提取公因式${3}^{n}$，因为当$n$趋向于无穷大时，${3}^{n}$的增长速度远快于${2}^{n}$，所以提取${3}^{n}$有助于简化极限计算。
步骤 2：简化表达式
提取公因式后，分子变为${3}^{n}(\dfrac{{2}^{n+1}}{{3}^{n}}+3)$，分母变为${3}^{n}(\dfrac{{2}^{n}}{{3}^{n}}+1)$。由于${3}^{n}$在分子和分母中都存在，可以相互约去。
步骤 3：计算极限
分子变为$\dfrac{{2}^{n+1}}{{3}^{n}}+3$，分母变为$\dfrac{{2}^{n}}{{3}^{n}}+1$。当$n$趋向于无穷大时，$\dfrac{{2}^{n+1}}{{3}^{n}}$和$\dfrac{{2}^{n}}{{3}^{n}}$都趋向于0，因此极限值为$\dfrac{0+3}{0+1}=3$。
观察分子和分母，可以提取公因式${3}^{n}$，因为当$n$趋向于无穷大时，${3}^{n}$的增长速度远快于${2}^{n}$，所以提取${3}^{n}$有助于简化极限计算。
步骤 2：简化表达式
提取公因式后，分子变为${3}^{n}(\dfrac{{2}^{n+1}}{{3}^{n}}+3)$，分母变为${3}^{n}(\dfrac{{2}^{n}}{{3}^{n}}+1)$。由于${3}^{n}$在分子和分母中都存在，可以相互约去。
步骤 3：计算极限
分子变为$\dfrac{{2}^{n+1}}{{3}^{n}}+3$，分母变为$\dfrac{{2}^{n}}{{3}^{n}}+1$。当$n$趋向于无穷大时，$\dfrac{{2}^{n+1}}{{3}^{n}}$和$\dfrac{{2}^{n}}{{3}^{n}}$都趋向于0，因此极限值为$\dfrac{0+3}{0+1}=3$。