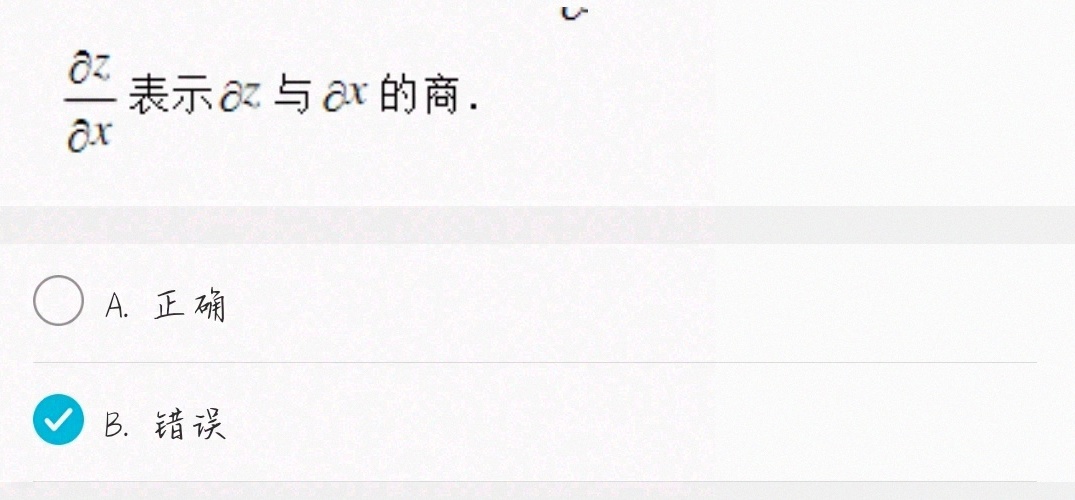
dfrac (partial z)(partial x) 表示az与ax的商.-|||-bigcirc A.正确-|||-B.错误

步骤 1：理解偏导数的定义
偏导数 $\dfrac {\partial z}{\partial x}$ 表示函数 $z$ 关于变量 $x$ 的变化率，即在保持其他变量不变的情况下，$z$ 对 $x$ 的变化率。它是一个整体的概念，不能简单地看作是两个量的商。

步骤 2：分析偏导数的表示
偏导数 $\dfrac {\partial z}{\partial x}$ 的表示形式类似于导数的表示形式，但它们的含义不同。导数 $\dfrac {dz}{dx}$ 可以看作是 $dz$ 与 $dx$ 的商，而偏导数 $\dfrac {\partial z}{\partial x}$ 不可以这样理解，因为偏导数是一个整体的概念，表示的是函数在某一点处关于一个变量的变化率。

步骤 3：判断题目的正确性
根据偏导数的定义和表示形式，$\dfrac {\partial z}{\partial x}$ 不能简单地看作是 $dz$ 与 $dx$ 的商，因此题目中的说法是错误的。