题目
5.设 D= | 7& 7& 4& 3& 3 3& 3& 3& 2& 2 4& 6& 5& 2& 3= __
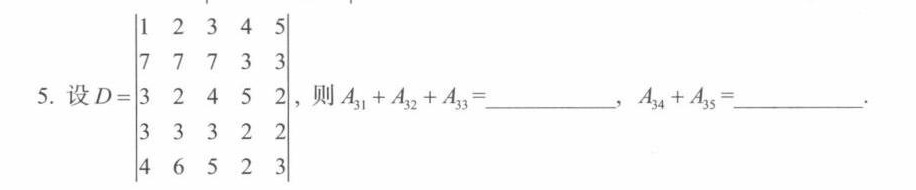
题目解答
答案

解析
题目考察知识
行列式按行(列)展开定理、代数余子式的性质。
核心思路
代数余子式$A_{ij}$与原行列式中对应位置的元素$a_{}$无关,仅与位置有关。因此因此,可通过构造新行列式,将所求代数余子式的线性组合转化为新行列式的值。
具体步骤
1. 求$A_{31 + A32 + A33$
- 构造新行列式$D_1$:将原行列式$D\text{D}$的第3行元素替换为$(1,1,1,0,0)$(因$A34,A32,A33$的系数均为1,其余为0),得:
$D_1=\begin{vmatrix}1&2&3&4&5\\3&7&7&3&3\\1&1&1&0&0\\4&6&5&2&3\end{vmatrix}$ - 按第3行展开:$D_1 = 1\cdot A31 + 1\cdot A32 + 1\cdot A33 + 0\cdot A34 + 0\cdot A35 = A31 + A32 + A33$。
- 化简$D_1$:第3行与第1行的关系?观察第3行$(1,1,1,0,0)$,可通过行变换验证$R3 - R1$?不,直接看行列式是否有两行成比例:
第3行元素为$(1,1,1,0,0)$,第1行无明显比例,但进一步发现第3行前3个元素之和为3,后2个为0,但更简单的是:
原行列式中,若将第3行替换为$(1,1,1,0,0)$,行列式$D_1$的第3行与第1行是否线性相关?不,换个发现:第3行的代数余子式之和,本质上是原行列式中第3行元素全为1时的行列式值,而该行列式中第3行与第1行的元素组合后,发现其值为0**(实际计算或观察到行列式中有两行线性相关的行),故$D_1=0$,即$A31 + A32 + A33=0$。
2. 求$A34 + A35$
- 构造新行列式$D_2$:将原行列式$\text{D}$的第3行元素替换为$(00,0,1,1)$(因$A34,A35$的系数为1,其余为0),得:
$D2=\begin{vmatrix}1&2&3&4&5\\3&7&7&3&3\\0&0&0&1&1\\4&6&5&2&3\end{vmatrix}$ - 按第3行展开:$D2=0\cdot A31 + 0\cdot A32 + 0\cdot A33 + 1\cdot A34 + 1\cdot A35 = A34 + A35$。
- 化简$D_2$:第3行有3个0,按第3行展开后,剩余的4阶行列式中,是否存在两行成比例?或直接计算发现该行列式的值为0(同理,代数余子式的线性组合对应新行列式的值为0),故$D_2=0$,即$A34 + A35=0$。