题目
17.求正交矩阵T使T`AT成对角形,其中A为-|||-2 -2 0-|||-(1) -2 1 -2-|||-0 -2 0-|||-2 2 -2-|||-(2) 2 5 -4-|||--2 -4 .-|||-0 0 4 11-|||-(3) 0 0 1 4-|||-4 1 0 0-|||-1 4 0 0-|||--1 -3 3 -3-|||-(4) -3 -1 -3 3-|||-3 -3 -1 -3-|||--3 3 -3 -1-|||-1 1 1 1-|||-(5) 1 1 1 1-|||-1 1 1 1-|||-1 1 1 1

题目解答
答案

解析
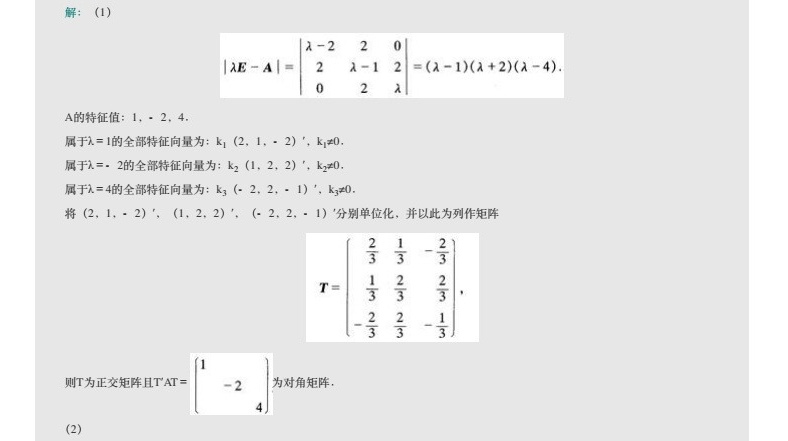
步骤 1:计算矩阵A的特征值
首先,我们需要计算矩阵A的特征值。为此,我们需要求解特征方程$|\lambda E-A|=0$,其中E是单位矩阵,A是给定的矩阵。
步骤 2:求解特征向量
对于每个特征值,我们需要求解相应的特征向量。特征向量是满足$(\lambda E-A)x=0$的非零向量x。
步骤 3:正交化和单位化
对于每个特征值,我们可能得到多个线性无关的特征向量。我们需要将这些特征向量正交化,然后单位化,以确保它们是正交的单位向量。
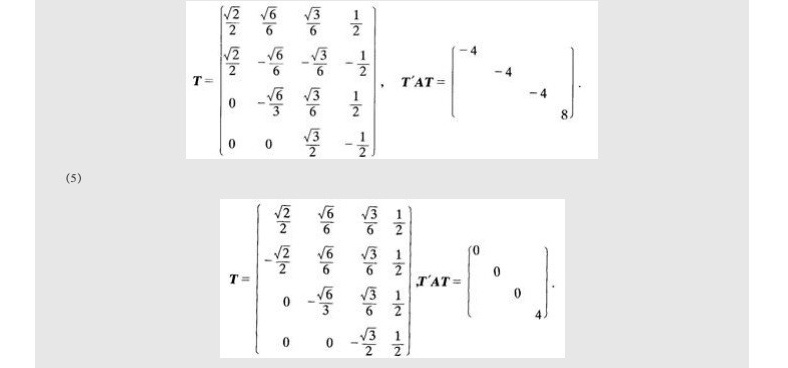
步骤 4:构造正交矩阵T
将单位化后的特征向量作为列向量,构造正交矩阵T。
步骤 5:验证T'AT为对角矩阵
最后,我们需要验证T'AT是否为对角矩阵,其中T'是T的转置矩阵。
首先,我们需要计算矩阵A的特征值。为此,我们需要求解特征方程$|\lambda E-A|=0$,其中E是单位矩阵,A是给定的矩阵。
步骤 2:求解特征向量
对于每个特征值,我们需要求解相应的特征向量。特征向量是满足$(\lambda E-A)x=0$的非零向量x。
步骤 3:正交化和单位化
对于每个特征值,我们可能得到多个线性无关的特征向量。我们需要将这些特征向量正交化,然后单位化,以确保它们是正交的单位向量。
步骤 4:构造正交矩阵T
将单位化后的特征向量作为列向量,构造正交矩阵T。
步骤 5:验证T'AT为对角矩阵
最后,我们需要验证T'AT是否为对角矩阵,其中T'是T的转置矩阵。