题目
已知P(A)=0.7,P(A)=0.7,P(A)=0.7,求P(A)=0.7.
已知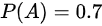 ,
,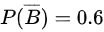 ,
,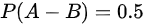 ,求
,求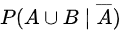 .
.
题目解答
答案
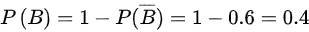 ,
,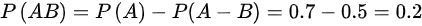 ,则
,则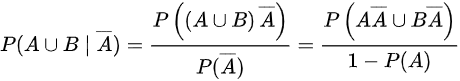
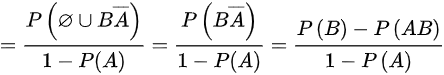
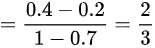 .
.
解析
考查要点:本题主要考查条件概率、事件运算及概率公式的综合应用,涉及事件的补集、差集、并集等运算,以及条件概率的定义和分解技巧。
解题核心思路:
- 利用补集概率求P(B):由$P(\overline{B})=0.6$可得$P(B)=1-0.6=0.4$。
- 通过差集公式求$P(A \cap B)$:根据$P(A-B)=P(A)-P(A \cap B)$,代入已知数据求出交集概率。
- 分解条件概率的分子:将$P((A \cup B) \cap \overline{A})$转化为$P(B \cap \overline{A})$,并利用概率加法公式进一步简化。
- 代入条件概率公式:最终通过分子分母的计算得到结果。
破题关键点:
- 正确理解事件运算关系:明确$(A \cup B) \cap \overline{A} = B \cap \overline{A}$。
- 灵活运用概率公式:如差集公式、条件概率公式及事件分解技巧。
步骤1:求$P(B)$
由$P(\overline{B})=0.6$,根据补集概率公式:
$P(B) = 1 - P(\overline{B}) = 1 - 0.6 = 0.4$
步骤2:求$P(A \cap B)$
根据差集公式$P(A-B) = P(A) - P(A \cap B)$,代入已知数据:
$0.5 = 0.7 - P(A \cap B) \implies P(A \cap B) = 0.7 - 0.5 = 0.2$
步骤3:分解条件概率的分子
目标概率为:
$P(A \cup B | \overline{A}) = \frac{P((A \cup B) \cap \overline{A})}{P(\overline{A})}$
其中:
- 分子分解:$(A \cup B) \cap \overline{A} = (A \cap \overline{A}) \cup (B \cap \overline{A}) = B \cap \overline{A}$(因$A \cap \overline{A} = \emptyset$)
- 进一步简化:$P(B \cap \overline{A}) = P(B) - P(A \cap B) = 0.4 - 0.2 = 0.2$
步骤4:计算分母
$P(\overline{A}) = 1 - P(A) = 1 - 0.7 = 0.3$
步骤5:代入公式求结果
$P(A \cup B | \overline{A}) = \frac{0.2}{0.3} = \frac{2}{3}$