题目
曲线=dfrac (x(x-1))(x(x-1)(x-2))的渐近线共有（ ）A.1条B.2条C.3条D.4条
曲线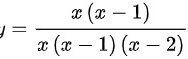
的渐近线共有（ ）
A.1条
B.2条
C.3条
D.4条
题目解答
答案
当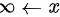
时，
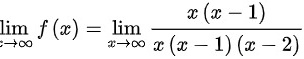
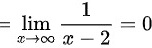，所以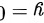
为一条水平渐近线，当
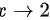时，
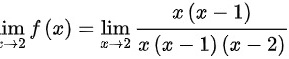
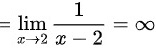，所以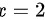
为一条铅直渐近线，综上所述，共有两条渐近线。所以本题选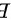
解析
步骤 1：确定水平渐近线
当$x\rightarrow \infty$时，$\lim _{x\rightarrow \infty }f(x)=\lim _{x\rightarrow \infty }\dfrac {x(x-1)}{x(x-1)(x-2)}$$=\lim _{x\rightarrow \infty }\dfrac {1}{x-2}=0$，所以$y=0$为一条水平渐近线。
步骤 2：确定铅直渐近线
当$x\rightarrow 2$时，$\lim _{x\rightarrow 2}f(x)=\lim _{x\rightarrow 2}\dfrac {x(x-1)}{x(x-1)(x-2)}$$=\lim _{x\rightarrow 2}\dfrac {1}{x-2}=\infty $，所以$x=2$为一条铅直渐近线。
步骤 3：总结渐近线数量
综上所述，共有两条渐近线。
当$x\rightarrow \infty$时，$\lim _{x\rightarrow \infty }f(x)=\lim _{x\rightarrow \infty }\dfrac {x(x-1)}{x(x-1)(x-2)}$$=\lim _{x\rightarrow \infty }\dfrac {1}{x-2}=0$，所以$y=0$为一条水平渐近线。
步骤 2：确定铅直渐近线
当$x\rightarrow 2$时，$\lim _{x\rightarrow 2}f(x)=\lim _{x\rightarrow 2}\dfrac {x(x-1)}{x(x-1)(x-2)}$$=\lim _{x\rightarrow 2}\dfrac {1}{x-2}=\infty $，所以$x=2$为一条铅直渐近线。
步骤 3：总结渐近线数量
综上所述，共有两条渐近线。