题目
2.在六阶行列式中,项a32a54 a41a65 a13a26所带的符号是 __
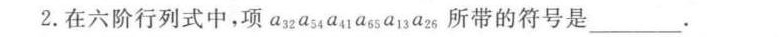
题目解答
答案
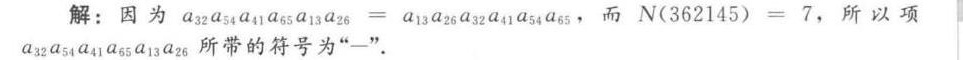
解析
步骤 1:确定排列的逆序数
首先,我们需要确定排列的逆序数。逆序数是指排列中所有逆序对的个数。逆序对是指排列中两个元素的位置与它们的大小顺序相反,即较大的元素在较小的元素前面。对于排列 362145,我们计算逆序数 N(362145)。
步骤 2:计算逆序数
计算排列 362145 的逆序数。逆序数 N(362145) = 7。具体计算如下:
- 3 和 2, 1, 4, 5 形成逆序对,共 4 个;
- 6 和 2, 1, 4, 5 形成逆序对,共 4 个;
- 2 和 1 形成逆序对,共 1 个;
- 4 和 5 形成逆序对,共 1 个;
- 5 没有逆序对。
步骤 3:确定符号
根据逆序数的奇偶性确定符号。如果逆序数是奇数,则符号为负;如果逆序数是偶数,则符号为正。因为 N(362145) = 7 是奇数,所以符号为负。
首先,我们需要确定排列的逆序数。逆序数是指排列中所有逆序对的个数。逆序对是指排列中两个元素的位置与它们的大小顺序相反,即较大的元素在较小的元素前面。对于排列 362145,我们计算逆序数 N(362145)。
步骤 2:计算逆序数
计算排列 362145 的逆序数。逆序数 N(362145) = 7。具体计算如下:
- 3 和 2, 1, 4, 5 形成逆序对,共 4 个;
- 6 和 2, 1, 4, 5 形成逆序对,共 4 个;
- 2 和 1 形成逆序对,共 1 个;
- 4 和 5 形成逆序对,共 1 个;
- 5 没有逆序对。
步骤 3:确定符号
根据逆序数的奇偶性确定符号。如果逆序数是奇数,则符号为负;如果逆序数是偶数,则符号为正。因为 N(362145) = 7 是奇数,所以符号为负。