题目
甲、乙两艘油轮驶向一个不能同时停泊两艘油轮的码头,它们都将在某日8时至20时抵达码头,甲轮卸完油要1小时,乙轮要2小时,假设毎艘油轮在8时至20时的毎一时刻抵达码头的可能性相同。求: 1.甲、乙两轮都不需要等候空出码头的概率; 2.设A表示甲、乙同一时刻抵达码头,问A是否为不可能事件,并求P(A)。
甲、乙两艘油轮驶向一个不能同时停泊两艘油轮的码头,它们都将在某日8时至20时抵达码头,甲轮卸完油要1小时,乙轮要2小时,假设毎艘油轮在8时至20时的毎一时刻抵达码头的可能性相同。求: 1.甲、乙两轮都不需要等候空出码头的概率; 2.设A表示甲、乙同一时刻抵达码头,问A是否为不可能事件,并求P(A)。
题目解答
答案
(1)设X、Y分别表示甲、乙两轮到达码头的时刻,则X、Y可以取区间[0,12]内的任意一个值,即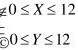 ,而两轮都不需要空出码头(用A表示)的充要条件是:Yndash;Xge;1或Xndash;Yge;2,在平面上建立直角坐标系(如图),
,而两轮都不需要空出码头(用A表示)的充要条件是:Yndash;Xge;1或Xndash;Yge;2,在平面上建立直角坐标系(如图),
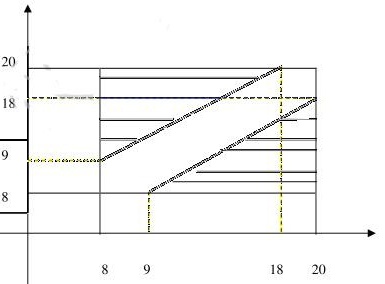 两轮都不需要空出码头的时间如图中阴影部分所示,这是一个几何概率问题,所以
两轮都不需要空出码头的时间如图中阴影部分所示,这是一个几何概率问题,所以
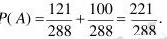 (2)A不是不可能事件,故P(A)=0。
(2)A不是不可能事件,故P(A)=0。
解析
考查要点:本题属于几何概率问题,考查学生对连续型概率模型的理解,以及如何将实际问题转化为几何区域面积比的能力。
解题核心思路:
- 建立坐标系:将甲、乙两轮的到达时间分别设为$x$和$y$,在$[0,12]$区间内均匀分布,构建直角坐标系。
- 确定不冲突条件:甲、乙不需要等待的条件是两者的到达时间间隔足够覆盖卸油时间,即$|x - y| \geq 1$(甲先到)或$|x - y| \geq 2$(乙先到)。
- 几何概率计算:通过计算满足条件的区域面积占总区域面积的比例求解。
破题关键点:
- 正确划分区域:明确甲、乙卸油时间对时间间隔的要求,画出对应的几何区域。
- 面积计算技巧:利用三角形、梯形面积公式简化积分计算。
第(1)题
条件分析:
甲、乙两轮不需要等待的条件是:
- 若甲先到,则乙到达时间至少比甲晚1小时,即$y \geq x + 1$;
- 若乙先到,则甲到达时间至少比乙晚2小时,即$x \geq y + 2$。
几何区域划分:
- 甲先到的区域:$y \geq x + 1$,对应直角坐标系中的一条斜线,下方为无效区域。
- 乙先到的区域:$x \geq y + 2$,对应另一条斜线,右侧为无效区域。
面积计算:
- 甲先到区域面积:
当$x$从$0$到$11$时,$y$的范围是$[x+1, 12]$,形成底为$11$、高为$11$的三角形,面积为$\frac{1}{2} \times 11 \times 11 = 60.5$。 - 乙先到区域面积:
当$y$从$0$到$10$时,$x$的范围是$[y+2, 12]$,形成底为$10$、高为$10$的三角形,面积为$\frac{1}{2} \times 10 \times 10 = 50$。 - 总面积:$60.5 + 50 = 110.5$。
概率计算:
总区域面积为$12 \times 12 = 144$,概率为$\frac{110.5}{144} = \frac{221}{288}$。
第(2)题
事件性质判断:
甲、乙同一时刻到达($x = y$)在连续型均匀分布中是零概率事件,但并非不可能事件(存在可能性,只是概率为0)。
概率计算:
由于$x$和$y$是连续型变量,$P(x = y) = 0$。