题目
(6)设随机变量X的分布律为 X=k =dfrac (c)(k!)(e)^-2 .=0,1,2, ···,则常数 c= __ .
题目解答
答案
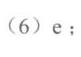
解析
本题考查利用随机变量分布律的性质求常数 $c$。随机变量的分布律需满足所有概率之和为1,即概率的规范性:$\sum_{k=0}^{\infty} P\{X=k\}=1$。
步骤1:写出概率和的表达式
已知 $P\{X=k\}=\frac{c}{k!}e^{-2}$($k=0,1,2,\cdots$),根据规范性有:
$\sum_{k=0}^{\infty} \frac{c}{k!}e^{-2} = 1$
步骤2:提取常数因子
常数 $c$ 和 $e^{-2}$ 可提取到求和符号外:
$c e^{-2} \sum_{k=0}^{\infty} \frac{1}{k!} = 1$
步骤3:利用泰勒展开公式
指数函数 $e^x$ 的泰勒展开式为:
$e^x = \sum_{k=0}^{\infty} \frac{x^k}{k!} \quad (-\infty < x < +\infty)$
令 $x=1$,得:
$\sum_{k=0}^{\infty} \frac{1}{k!} = e^1 = e$
步骤4:求解 $c$
代入求和结果:
$c e^{-2} \cdot e = 1 \implies c e^{-1} = 1 \implies c = e$