题目
设(x,y,z)=(x)^2+(y)^3+z,求(x,y,z)=(x)^2+(y)^3+z,在点(x,y,z)=(x)^2+(y)^3+z,处沿方向(x,y,z)=(x)^2+(y)^3+z,的方向导数
设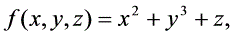 求
求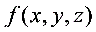 在点
在点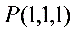 处沿方向
处沿方向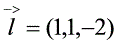 的方向导数
的方向导数
题目解答
答案
解 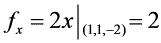
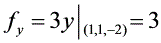
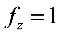
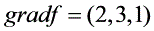
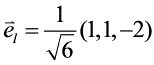
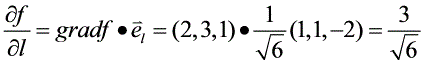
解析
本题考查多元函数方向导数的计算,解题思路是先求出函数在给定点处的偏导数,得到梯度向量,再求出给定方向的单位向量,最后将梯度向量与单位向量做点积,得到方向导数。
下面我们一步一步进行计算:
- 求函数$f(x,y,z)$在点$P(1,1,1)$处的偏导数:
- 对$x$求偏导数:${f}_{x}=\frac{\partial f}{\partial x}=2x$,将点$P(1,1,1)$的$x = 1$代入,得到${f}_{x}\big|_{(1,1,1)} = 2\times1 = 2$。
- 对$y$求偏导数:${f}_{y}=\frac{\partial f}{\partial y}=3y^{2}$,将点$P(1,1,1)$的$y = 1$代入,得到${f}_{y}\big|_{(1,1,1)} = 3\times1^{2}= 3$。
- 对$z$求偏导数:${f}_{z}=\frac{\partial f}{\partial z}=1$。
- 得到梯度向量$\text{grad}f$:
梯度向量$\text{grad}f = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})$,将上面求得的偏导数代入,得到$\text{grad}f\big|_{(1,1,1)} = (2,3,1)$。 - 求方向$\overrightarrow{i}=(1,1,-2)$的单位向量$\overrightarrow{e}$:
单位向量$\overrightarrow{e}=\frac{\overrightarrow{i}}{\vert\overrightarrow{i}\vert}$,其中$\vert\overrightarrow{i}\vert=\sqrt{1^{2}+1^{2}+(-2)^{2}}=\sqrt{1 + 1 + 4}=\sqrt{6}$。
所以$\overrightarrow{e}=\frac{1}{\sqrt{6}}(1,1,-2)$。 - 求方向导数$\frac{\partial f}{\partial l}$:
方向导数$\frac{\partial f}{\partial l}=\text{grad}f\cdot\overrightarrow{e}$,将梯度向量$\text{grad}f = (2,3,1)$和单位向量$\overrightarrow{e}=\frac{1}{\sqrt{6}}(1,1,-2)$代入,得到:
$\frac{\partial f}{\partial l}=(2,3,1)\cdot\frac{1}{\sqrt{6}}(1,1,-2)=\frac{2\times1 + 3\times1 + 1\times(-2)}{\sqrt{6}}=\frac{2 + 3 - 2}{\sqrt{6}}=\frac{3}{\sqrt{6}}$。