题目
求过点 M0(1,1,0)且与直线 dfrac (x-1)(2)=dfrac (y)(1)=dfrac (z)(2) 垂直相交的直线方程.(8分)
求过点 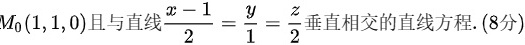
题目解答
答案
解:由题可知,
解析
步骤 1:确定垂直条件
直线 $\dfrac {x-1}{2}=\dfrac {y}{1}=\dfrac {z}{2}$ 的方向向量为 $\vec{d}=(2,1,2)$。要求的直线与之垂直,因此其方向向量 $\vec{d_1}$ 应满足 $\vec{d} \cdot \vec{d_1} = 0$。
步骤 2:确定平面方程
由于要求的直线与给定直线垂直相交,可以先找到一个包含给定直线且通过点 M0(1,1,0) 的平面。该平面的法向量为 $\vec{d}=(2,1,2)$,因此平面方程为 $2x+y+2z=a$。将点 M0(1,1,0) 代入,得 $2*1+1*1+2*0=a$,解得 $a=3$。所以平面方程为 $2x+y+2z=3$。
步骤 3:求交点
将直线 $\dfrac {x-1}{2}=\dfrac {y}{1}=\dfrac {z}{2}$ 的参数方程代入平面方程 $2x+y+2z=3$,得 $2(1+2t)+t+2(2t)=3$,解得 $t=\dfrac{1}{9}$。将 $t=\dfrac{1}{9}$ 代入直线的参数方程,得交点坐标为 $(\dfrac{11}{9},\dfrac{1}{9},\dfrac{2}{9})$。
步骤 4:确定方向向量
方向向量为点 M0(1,1,0) 与交点 $(\dfrac{11}{9},\dfrac{1}{9},\dfrac{2}{9})$ 的向量,即 $(\dfrac{11}{9}-1,\dfrac{1}{9}-1,\dfrac{2}{9}-0)=(\dfrac{2}{9},\dfrac{-8}{9},\dfrac{2}{9})$。
步骤 5:写出直线方程
根据点 M0(1,1,0) 和方向向量 $(\dfrac{2}{9},\dfrac{-8}{9},\dfrac{2}{9})$,写出直线方程为 $\dfrac{x-1}{\dfrac{2}{9}}=\dfrac{y-1}{\dfrac{-8}{9}}=\dfrac{z}{\dfrac{2}{9}}$,化简得 $\dfrac{x-1}{1}=\dfrac{y-1}{-4}=\dfrac{z}{1}$。
直线 $\dfrac {x-1}{2}=\dfrac {y}{1}=\dfrac {z}{2}$ 的方向向量为 $\vec{d}=(2,1,2)$。要求的直线与之垂直,因此其方向向量 $\vec{d_1}$ 应满足 $\vec{d} \cdot \vec{d_1} = 0$。
步骤 2:确定平面方程
由于要求的直线与给定直线垂直相交,可以先找到一个包含给定直线且通过点 M0(1,1,0) 的平面。该平面的法向量为 $\vec{d}=(2,1,2)$,因此平面方程为 $2x+y+2z=a$。将点 M0(1,1,0) 代入,得 $2*1+1*1+2*0=a$,解得 $a=3$。所以平面方程为 $2x+y+2z=3$。
步骤 3:求交点
将直线 $\dfrac {x-1}{2}=\dfrac {y}{1}=\dfrac {z}{2}$ 的参数方程代入平面方程 $2x+y+2z=3$,得 $2(1+2t)+t+2(2t)=3$,解得 $t=\dfrac{1}{9}$。将 $t=\dfrac{1}{9}$ 代入直线的参数方程,得交点坐标为 $(\dfrac{11}{9},\dfrac{1}{9},\dfrac{2}{9})$。
步骤 4:确定方向向量
方向向量为点 M0(1,1,0) 与交点 $(\dfrac{11}{9},\dfrac{1}{9},\dfrac{2}{9})$ 的向量,即 $(\dfrac{11}{9}-1,\dfrac{1}{9}-1,\dfrac{2}{9}-0)=(\dfrac{2}{9},\dfrac{-8}{9},\dfrac{2}{9})$。
步骤 5:写出直线方程
根据点 M0(1,1,0) 和方向向量 $(\dfrac{2}{9},\dfrac{-8}{9},\dfrac{2}{9})$,写出直线方程为 $\dfrac{x-1}{\dfrac{2}{9}}=\dfrac{y-1}{\dfrac{-8}{9}}=\dfrac{z}{\dfrac{2}{9}}$,化简得 $\dfrac{x-1}{1}=\dfrac{y-1}{-4}=\dfrac{z}{1}$。