题目
设=ln sqrt (dfrac {1-x)(1-{x)^2}}则 dy|=ln sqrt (dfrac {1-x)(1-{x)^2}}
设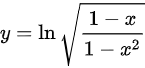 则 dy|
则 dy|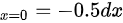
题目解答
答案
对函数进行化简
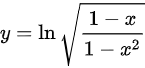
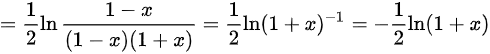 求微分,将ln(1+x)看成ln(f(x)),进行链式求导
求微分,将ln(1+x)看成ln(f(x)),进行链式求导
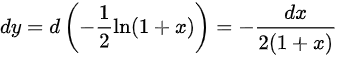
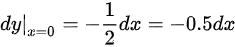
解析
考查要点:本题主要考查复合函数的微分运算,涉及对数函数的化简与求导法则。
解题核心思路:
- 化简原函数:利用分式约分和对数性质,将复杂表达式转化为简单形式,简化后续求导过程。
- 应用微分公式:对化简后的函数应用微分规则,特别注意链式法则的使用。
- 代入特定点:将$x=0$代入导数表达式,得到最终结果。
破题关键点:
- 分式约分:将分母$1-x^2$分解为$(1-x)(1+x)$,与分子约分后简化表达式。
- 对数性质:利用$\ln \frac{1}{a} = -\ln a$进一步化简函数。
- 导数计算:正确应用$\frac{d}{dx} \ln(1+x) = \frac{1}{1+x}$,并处理系数。
原函数化简:
$\begin{aligned}y &= \ln \sqrt{\dfrac{1-x}{1-x^2}} \\&= \dfrac{1}{2} \ln \dfrac{1-x}{(1-x)(1+x)} \quad \text{(平方根转化为指数形式)} \\&= \dfrac{1}{2} \ln \dfrac{1}{1+x} \quad \text{(约分后简化)} \\&= -\dfrac{1}{2} \ln(1+x) \quad \text{(应用对数性质$\ln \frac{1}{a} = -\ln a$)}\end{aligned}$
求微分:
对化简后的函数$y = -\dfrac{1}{2} \ln(1+x)$求微分:
$dy = -\dfrac{1}{2} \cdot \dfrac{1}{1+x} \, dx \quad \text{(链式法则直接应用)}$
代入$x=0$:
$dy|_{x=0} = -\dfrac{1}{2(0+1)} \, dx = -\dfrac{1}{2} \, dx = -0.5 \, dx$