题目
[题目]设 f(x)= ) 1,|x|lt 1 0,|x|=1 -1,|x|gt 1 .-|||-求f[g(x)]和g[f(x)],并作出这两个函数的图形。

题目解答
答案
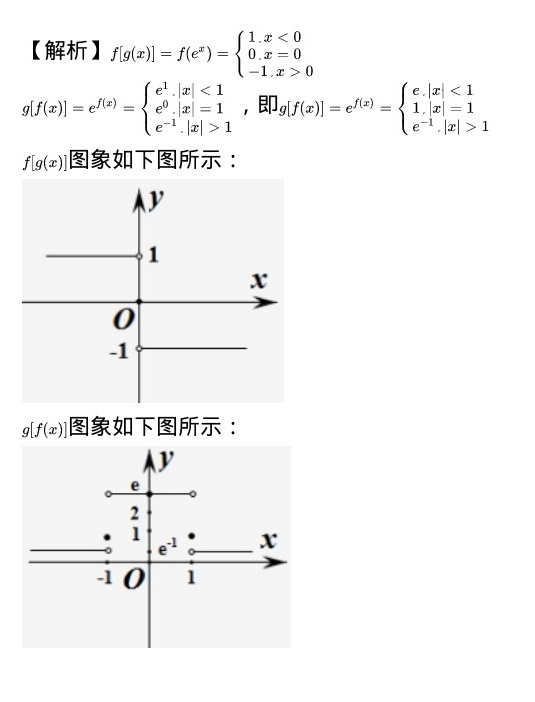
解析
考查要点:本题主要考查分段函数的复合运算及函数图像的绘制能力。需要理解如何将一个函数作为另一个函数的输入,并根据输入值的范围确定输出值。
解题核心思路:
- 复合函数定义:明确$f[g(x)]$表示将$g(x)$的输出作为$f(x)$的输入,同理$g[f(x)]$是将$f(x)$的输出作为$g(x)$的输入。
- 分段讨论:根据$f(x)$和$g(x)$的分段条件,分别分析不同区间内输入值对应的输出结果。
- 图像绘制:根据分段函数的表达式,分区间绘制对应的水平线或特定点。
破题关键点:
- $f[g(x)]$:通过分析$g(x)=e^x$的取值范围,确定$e^x$在$f(x)$定义域中的位置。
- $g[f(x)]$:直接利用$f(x)$的分段结果,代入指数函数$g(x)$中。
求$f[g(x)]$
-
分析$g(x)=e^x$的取值范围:
- 当$x < 0$时,$e^x < 1$;
- 当$x = 0$时,$e^x = 1$;
- 当$x > 0$时,$e^x > 1$。
-
代入$f(x)$的分段条件:
- 当$e^x < 1$(即$x < 0$),$f(e^x) = 1$;
- 当$e^x = 1$(即$x = 0$),$f(e^x) = 0$;
- 当$e^x > 1$(即$x > 0$),$f(e^x) = -1$。
结果:
$f[g(x)] =
\begin{cases} 1, & x < 0 \\0, & x = 0 \\-1, & x > 0 \end{cases}$
求$g[f(x)]$
-
分析$f(x)$的分段结果:
- 当$|x| < 1$时,$f(x) = 1$;
- 当$|x| = 1$时,$f(x) = 0$;
- 当$|x| > 1$时,$f(x) = -1$。
-
代入$g(x)=e^x$:
- 当$|x| < 1$时,$g(f(x)) = e^1 = e$;
- 当$|x| = 1$时,$g(f(x)) = e^0 = 1$;
- 当$|x| > 1$时,$g(f(x)) = e^{-1} = \frac{1}{e}$。
结果:
$g[f(x)] =
\begin{cases} e, & |x| < 1 \\1, & |x| = 1 \\\frac{1}{e}, & |x| > 1 \end{cases}$