题目
求曲面^2+xy-yz=1在点(1,0,1)处的切平面方程和法线方程。
求曲面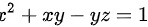 在点(1,0,1)处的切平面方程和法线方程。
在点(1,0,1)处的切平面方程和法线方程。
题目解答
答案
令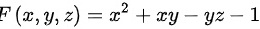
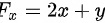 ,
,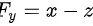 ,
,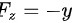
在点(1,0,1)处
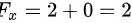 ,
,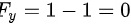
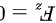
即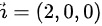
∴切平面方程为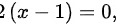 即
即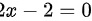
法线方程为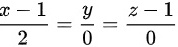
解析
步骤 1:求偏导数
首先,我们需要求出曲面${x}^{2}+xy-yz=1$在点(1,0,1)处的偏导数。设$F(x,y,z)={x}^{2}+xy-yz-1$,则有:
$F_x=2x+y$,
$F_y=x-z$,
$F_z=-y$.
步骤 2:计算偏导数值
在点(1,0,1)处,我们计算偏导数的值:
$F_x(1,0,1)=2*1+0=2$,
$F_y(1,0,1)=1-1=0$,
$F_z(1,0,1)=-0=0$.
步骤 3:求切平面方程
根据切平面方程的公式$F_x(x-x_0)+F_y(y-y_0)+F_z(z-z_0)=0$,代入点(1,0,1)和偏导数值,得到切平面方程:
$2(x-1)+0(y-0)+0(z-1)=0$,
化简得:$2x-2=0$.
步骤 4:求法线方程
根据法线方程的公式$\frac{x-x_0}{F_x}=\frac{y-y_0}{F_y}=\frac{z-z_0}{F_z}$,代入点(1,0,1)和偏导数值,得到法线方程:
$\frac{x-1}{2}=\frac{y-0}{0}=\frac{z-1}{0}$.
首先,我们需要求出曲面${x}^{2}+xy-yz=1$在点(1,0,1)处的偏导数。设$F(x,y,z)={x}^{2}+xy-yz-1$,则有:
$F_x=2x+y$,
$F_y=x-z$,
$F_z=-y$.
步骤 2:计算偏导数值
在点(1,0,1)处,我们计算偏导数的值:
$F_x(1,0,1)=2*1+0=2$,
$F_y(1,0,1)=1-1=0$,
$F_z(1,0,1)=-0=0$.
步骤 3:求切平面方程
根据切平面方程的公式$F_x(x-x_0)+F_y(y-y_0)+F_z(z-z_0)=0$,代入点(1,0,1)和偏导数值,得到切平面方程:
$2(x-1)+0(y-0)+0(z-1)=0$,
化简得:$2x-2=0$.
步骤 4:求法线方程
根据法线方程的公式$\frac{x-x_0}{F_x}=\frac{y-y_0}{F_y}=\frac{z-z_0}{F_z}$,代入点(1,0,1)和偏导数值,得到法线方程:
$\frac{x-1}{2}=\frac{y-0}{0}=\frac{z-1}{0}$.