题目
7.已知 a=2i-3j+k =i-overline (j)+3k =i-2j. 计算-|||-(1) (acdot b)c-(acdot c)b;
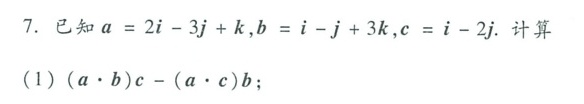
题目解答
答案

解析
考查要点:本题主要考查向量的点积运算和向量的线性组合运算。
解题思路:
- 先计算两个点积:$\overrightarrow{a} \cdot \overrightarrow{b}$ 和 $\overrightarrow{a} \cdot \overrightarrow{c}$,这两个结果都是标量。
- 将标量分别与向量$\overrightarrow{c}$和$\overrightarrow{b}$相乘,得到两个向量。
- 对两个向量进行减法运算,最终得到结果。
关键点:注意点积的计算规则和向量的分量运算,避免符号错误。
第(1)题
计算$\overrightarrow{a} \cdot \overrightarrow{b}$
根据点积公式:
$\overrightarrow{a} \cdot \overrightarrow{b} = (2)(1) + (-3)(-1) + (1)(3) = 2 + 3 + 3 = 8$
计算$\overrightarrow{a} \cdot \overrightarrow{c}$
向量$\overrightarrow{c}$的$k$分量为$0$,因此:
$\overrightarrow{a} \cdot \overrightarrow{c} = (2)(1) + (-3)(-2) + (1)(0) = 2 + 6 + 0 = 8$
计算$8\overrightarrow{c}$和$8\overrightarrow{b}$
$8\overrightarrow{c} = 8(i - 2j) = 8i - 16j$
$8\overrightarrow{b} = 8(i - j + 3k) = 8i - 8j + 24k$
向量减法
$8\overrightarrow{c} - 8\overrightarrow{b} = (8i - 16j) - (8i - 8j + 24k) = -8j - 24k$