题目
矩阵 与矩阵 相似,则其方幂矩阵也相似。( )正确错误
矩阵 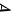 与矩阵
与矩阵 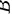 相似,则其方幂矩阵也相似。( )
相似,则其方幂矩阵也相似。( )
 正确
正确
 错误
错误
题目解答
答案
由矩阵相似的性质:
若 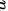 阶矩阵
阶矩阵 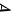 与
与 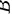 相似,则
相似,则 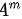 和
和 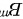 相似,其中
相似,其中 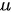 为非负整数
为非负整数
 矩阵
矩阵 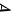 与矩阵
与矩阵 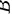 相似,则其方幂矩阵也相似
相似,则其方幂矩阵也相似
故选 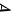
解析
步骤 1:定义相似矩阵
两个矩阵 和 相似,如果存在一个可逆矩阵 ,使得 。
步骤 2:方幂矩阵的相似性
如果矩阵 和 相似,即存在可逆矩阵 使得 ,则对于任意非负整数 ,有:
。
步骤 3:验证方幂矩阵的相似性
由步骤 2 可知,对于任意非负整数 ,有:
,
这表明矩阵 和 的方幂矩阵也相似。
两个矩阵 和 相似,如果存在一个可逆矩阵 ,使得 。
步骤 2:方幂矩阵的相似性
如果矩阵 和 相似,即存在可逆矩阵 使得 ,则对于任意非负整数 ,有:
。
步骤 3:验证方幂矩阵的相似性
由步骤 2 可知,对于任意非负整数 ,有:
,
这表明矩阵 和 的方幂矩阵也相似。