题目
5.设 =(e)^xcos 3x+(x)^x, 求y`。
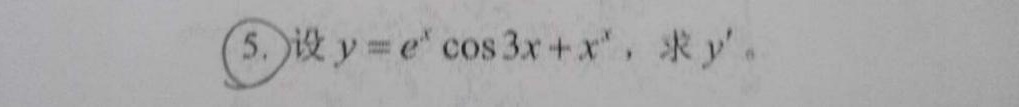
题目解答
答案

解析
步骤 1:求导 ${e}^{x}\cos 3x$
根据乘积法则,$(uv)'=u'v+uv'$,其中 $u={e}^{x}$,$v=\cos 3x$。因此,$u'={e}^{x}$,$v'=-3\sin 3x$。所以,${e}^{x}\cos 3x$ 的导数为 ${e}^{x}\cos 3x-3{e}^{x}\sin 3x$。
步骤 2:求导 ${x}^{x}$
使用对数求导法,设 $y={x}^{x}$,则 $\ln y=x\ln x$。对两边求导,得到 $\frac{1}{y}y'=1+\ln x$,因此 $y'={x}^{x}(1+\ln x)$。
步骤 3:合并结果
将步骤 1 和步骤 2 的结果合并,得到 $y'={e}^{x}\cos 3x-3{e}^{x}\sin 3x+{x}^{x}(1+\ln x)$。
根据乘积法则,$(uv)'=u'v+uv'$,其中 $u={e}^{x}$,$v=\cos 3x$。因此,$u'={e}^{x}$,$v'=-3\sin 3x$。所以,${e}^{x}\cos 3x$ 的导数为 ${e}^{x}\cos 3x-3{e}^{x}\sin 3x$。
步骤 2:求导 ${x}^{x}$
使用对数求导法,设 $y={x}^{x}$,则 $\ln y=x\ln x$。对两边求导,得到 $\frac{1}{y}y'=1+\ln x$,因此 $y'={x}^{x}(1+\ln x)$。
步骤 3:合并结果
将步骤 1 和步骤 2 的结果合并,得到 $y'={e}^{x}\cos 3x-3{e}^{x}\sin 3x+{x}^{x}(1+\ln x)$。