设非负函数y=y(x)(x≥0)满足微分方程xy"-y'+2=0,当曲线=y(x)过原点时,其与直线x=1及y=0围成平面区域D的面积为2,求D绕y轴旋转所得旋转体的体积.
题目解答
答案
解微分方程xy"-y'+2=0,得其通解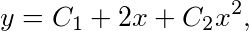 其中
其中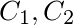 为任意常数,因为
为任意常数,因为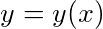 通过原点时与直线x=1及y=0围成平面的面积为2,于是,可得
通过原点时与直线x=1及y=0围成平面的面积为2,于是,可得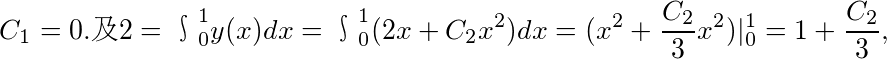
从而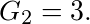
所求非负函数为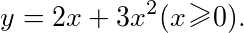
在第一象限曲线y=f(x)表示为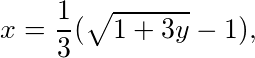 D绕y轴旋转所得旋转体的体积为
D绕y轴旋转所得旋转体的体积为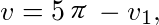 其中
其中
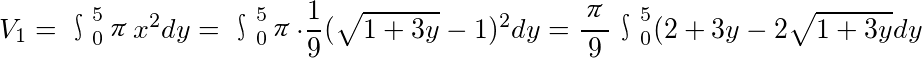 =
=
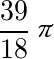 ,
,
所以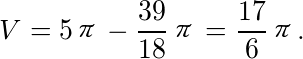
解析
考查要点:本题综合考查微分方程求解、定积分应用(面积与旋转体体积)。
解题思路:
- 解微分方程:通过变量替换降阶,求出通解,利用初始条件确定常数;
- 面积条件:通过积分计算区域面积,进一步确定未知常数;
- 旋转体体积:利用washer method(圆盘法),将体积表示为外体积与内体积之差,通过分部积分求解。
破题关键:
- 变量替换降阶:令$p = y'$,将二阶方程转化为一阶方程;
- 正确应用面积条件:明确积分上下限与被积函数;
- 体积计算方法选择:通过分析几何形状,选择washer method简化计算。
1. 解微分方程
令$p = y'$,则原方程$xy'' - y' + 2 = 0$变为:
$x \frac{dp}{dx} - p + 2 = 0 \implies \frac{dp}{dx} = \frac{p - 2}{x}$
分离变量积分:
$\int \frac{dp}{p - 2} = \int \frac{dx}{x} \implies \ln|p - 2| = \ln x + C \implies p = Cx + 2$
积分得通解:
$y = \int (Cx + 2) dx = \frac{C}{2}x^2 + 2x + C_1$
整理为:
$y = C_2 x^2 + 2x + C_1 \quad (\text{其中} C_2 = C/2)$
2. 确定常数
过原点条件:当$x = 0$时,$y = 0$,代入得$C_1 = 0$,通解简化为:
$y = C_2 x^2 + 2x$
面积条件:区域$D$的面积为$\int_0^1 y(x) dx = 2$,代入得:
$\int_0^1 (2x + C_2 x^2) dx = \left[ x^2 + \frac{C_2}{3}x^3 \right]_0^1 = 1 + \frac{C_2}{3} = 2 \implies C_2 = 3$
最终解为:
$y = 2x + 3x^2$
3. 计算旋转体体积
washer method:
- 外体积:由$x = 1$到$y = 5$形成的圆柱体积为$\pi \cdot 1^2 \cdot 5 = 5\pi$;
- 内体积:由曲线$y = 2x + 3x^2$围成的体积,需将$x$表示为$y$的函数:
$x = \frac{\sqrt{1 + 3y} - 1}{3}$
积分计算:
$V_1 = \pi \int_0^5 x^2 dy = \frac{\pi}{9} \int_0^5 \left( 2 + 3y - 2\sqrt{1 + 3y} \right) dy$
分项积分后得$V_1 = \frac{13}{6}\pi$; - 总旋转体体积:
$V = 5\pi - V_1 = 5\pi - \frac{13}{6}\pi = \frac{17}{6}\pi$