3.计算下列行列式:-|||-_(1)+(lambda )_(1) a2 an-|||-(1) a1 _(2)+(lambda )_(2) an-|||-((lambda )_(i)neq 0,i=1,2,... ,n) ;-|||-a1 a2 _(n)+(lambda )_(n)-|||-a1 a^(1-1)b1··· _(1)(b)_(1)-1 bπ-|||-a2 ({a)_(2)}^n-1(b)_(2) . _(2)(b)_(2)-1 b^n^2-|||-(2)-|||-((a)_(i)neq 0,i=1,2,... ,n+1).-|||-a ({a)_(n)}^n-1(b)_(n)... (a)_(n)({b)_(n)}^n-1 ^n-|||-^n+1 ({a)_(n+1)}^n(b)_(n+1) ···an+1bn+1 ^n+1

题目解答
答案
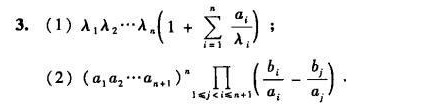
解析
(1)第一题考查要点
本题是一个对角占优的行列式,对角线元素为$a_i + \lambda_i$,其余元素为$a_i$。解题核心在于利用矩阵行列式引理,将原行列式分解为对角矩阵与秩一矩阵的和,从而快速计算。
(2)第二题考查要点
本题是一个复杂结构的行列式,涉及$a_i$和$b_i$的高次幂组合。解题关键在于提取公因子,将行列式分解为$(a_1a_2\cdots a_{n+1})^n$与另一行列式的乘积,再通过分式变形简化剩余部分。
第(1)题
行列式结构分析
原行列式可表示为:
$\begin{pmatrix}a_1 + \lambda_1 & a_2 & \cdots & a_n \\a_1 & a_2 + \lambda_2 & \cdots & a_n \\\vdots & \vdots & \ddots & \vdots \\a_1 & a_2 & \cdots & a_n + \lambda_n\end{pmatrix}$
应用矩阵行列式引理
令$D = \text{diag}(\lambda_1, \lambda_2, \dots, \lambda_n)$,向量$u = (a_1, a_2, \dots, a_n)^T$,$v = (1, 1, \dots, 1)^T$,则原行列式可写为$D + uv^T$。根据引理:
$\det(D + uv^T) = \det(D) \left(1 + v^T D^{-1} u \right)$
计算各部分
- $\det(D) = \lambda_1 \lambda_2 \cdots \lambda_n$
- $D^{-1}u = \left(\frac{a_1}{\lambda_1}, \frac{a_2}{\lambda_2}, \dots, \frac{a_n}{\lambda_n}\right)^T$
- $v^T D^{-1} u = \sum_{i=1}^n \frac{a_i}{\lambda_i}$
最终结果为:
$\lambda_1 \lambda_2 \cdots \lambda_n \left(1 + \sum_{i=1}^n \frac{a_i}{\lambda_i}\right)$
第(2)题
行列式结构分析
原行列式为$(n+1)$阶,形式复杂。通过观察每一行的元素,发现可提取公因子$a_i^n$,剩余部分为关于$\frac{b_i}{a_i}$的行列式。
提取公因子
将第$i$行提取$a_i^n$,行列式变为:
$(a_1a_2\cdots a_{n+1})^n \cdot \begin{vmatrix}1 & \frac{b_1}{a_1} & \cdots & \left(\frac{b_1}{a_1}\right)^{n} \\\vdots & \vdots & \ddots & \vdots \\1 & \frac{b_{n+1}}{a_{n+1}} & \cdots & \left(\frac{b_{n+1}}{a_{n+1}}\right)^{n}\end{vmatrix}$
范德蒙德行列式变形
剩余行列式为范德蒙德行列式的变形,其值为:
$\prod_{1 \leq i < j \leq n+1} \left(\frac{b_j}{a_j} - \frac{b_i}{a_i}\right)$
最终结果为:
$(a_1a_2\cdots a_{n+1})^n \cdot \prod_{1 \leq i < j \leq n+1} \left(\frac{b_j}{a_j} - \frac{b_i}{a_i}\right)$